First note that $f\in\operatorname{Diff}^r(M)$ generates a group action of $\mathbb{Z}$ on $M$:
$$a_\bullet:\mathbb{Z}\to\operatorname{Diff}^r(M), n\mapsto [x\mapsto f^n(x)=f\circ f\circ \cdots f(x)]\quad (\text{ $ n$ times composition}).$$
By calling $a_\bullet$ a group action of $\mathbb{Z}$ I mean that $a_\bullet$ is a family of diffeomorphisms of $M$ parameterized by integers with the property that $a_{n+m}=a_n\circ a_m$.
Typically the word "flow" refers to a group action of $\mathbb{R}$. Here the horizontal flow is:
$$g_\bullet:\mathbb{R}\to\operatorname{Diff}^r(\mathbb{R}\times M), t\mapsto [(s,x)\mapsto (t+s,x)],$$
that is, $g_t(s,x)=(t+s,x)$. Again, saying that $g_\bullet$ is a group action of $\mathbb{R}$ means that it is a family of diffeomorphisms of $\mathbb{R}\times M$ parameterized by real numbers with the property that $g_{t_1+t_2}=g_{t_1}\circ g_{t_2}$.
Like you say $g_\bullet$ factors through the equivalence relation $\sim$ you stated and gives a flow
$$\phi_\bullet:\mathbb{R}\to \operatorname{Diff}^r(\mathbb{R}\times M/\sim).$$
The points of $\mathbb{R}\times M/\sim$ are equivalence classes $[s,x]$ of points $(s,x)$ in $\mathbb{R}\times M$, that is,
$$[s_1,x_1]=[s_2,x_2] \iff \exists n\in\mathbb{Z}: s_2=s_1-n, x_2=f^n(x_1).$$
Writing $\phi_t([s,x])=[t+s,x]$ is unambiguous ($\dagger$), and $\phi_{t_1+t_2}=\phi_{t_1}\circ\phi_{t_2}$.
Let me also mention that instead of writing $\alpha_\bullet:G\to \operatorname{Diff}^r(M)$ for a group $G$ acting on a manifold $M$ by $C^r$ diffeomorphisms alternatively one could write $\alpha: G\times M\to M, (t,x)\mapsto \alpha_t(x)$, which is the notation you are using.
For a flow $\phi_\bullet:\mathbb{R}\to\operatorname{Diff}^r(M)$ and for a fixed $t\in\mathbb{R}$, $\phi_t\in\operatorname{Diff}^r(M)$ is called the time-$t$ map of $\phi$. So the time-$1$ map of $\phi_\bullet$ is $\phi_1$.
$\phi_\bullet$ is defined by ($\dagger$) above. I'll leave it to you to verify that indeed this definition is unambiguous, that is, this definition does not depend on the choice of representatives (i.e. $[s_1,x_1]=[s_2,x_2]\implies \phi_t([s_1,x_1])=\phi_t([s_2,x_2])$).
See 1..
In dynamics literature typically $C^r$ conjugacy between two actions $\alpha_\bullet:G\to \operatorname{Diff}^r(X)$ and $\beta_\bullet: G\to \operatorname{Diff}^r(Y)$ refers to a $C^r$ diffeomorphism $H:X\to Y$ such that for any $t\in G: H\circ \alpha_t=\beta_t\circ H$. So the underlying manifolds ought to be of the same dimension. But
$$\dim(\mathbb{R}\times M/\sim)=1+\dim(M),$$
as you stated, so $\phi_1$ is not $C^r$ (nor $C^0$) conjugate to $f$.
If we only require $H$ to be a $C^r$ map (not necessarily with an inverse), then $\alpha_\bullet$ is said to be $C^r$ semi-conjugate to $\beta_\bullet$. In this situation, $f$ is indeed $C^r$ semi-conjugate to $\phi_1$. To see this first note that we need a $C^r$ map $H: M\to \mathbb{R}\times M/\sim$ such that $H\circ f=\phi_1\circ H$:
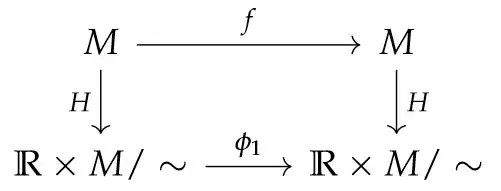
To find such an $H$ first note how $\phi_1$ acts on $\mathbb{R}\times M/\sim$:
$$\phi_1([s,x])=[1+s,x]=[s+1,x]=[s,f(x)],$$
that is, even though $\phi_\bullet$ descends from a "horizontal" flow (and this adjective indeed has significance), its time-$1$ map acts "vertically" (no matter what $s$ is chosen). So putting $H(p)=[s_p,x_p]$, we need $H$ to satisfy
$$[s_p,f(x_p)]=[s_{f(p)},x_{f(p)}].$$
I hope this much is enough for you to find such an $H$ (in this case there are many choices; for a general group action there is only one guaranteed by construction).
