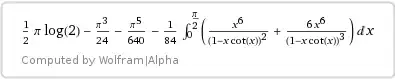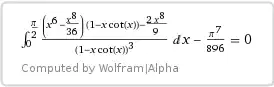$\color{brown}{\textbf{Alternative expressions for the integral.}}$
Firstly,
$$I = \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\ln(1-x\cot x)\,\mathrm dx
= \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\ln(\sin x - x\cos x)\,\mathrm dx
- \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\ln(\sin x)\,\mathrm dx = \dfrac\pi2\ln2 +I_1,$$
wherein $I_1$ allows integration by parts:
$$I_1 = \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\ln(\sin x - x\cos x)\,\mathrm dx
= x\ln(\sin x-x\cos x)\bigg|_{\ 0}^{\Large^\pi\hspace{-1pt}/_2}
- \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^2\sin x}{\sin x - x\cos x}\,\mathrm dx,$$
$$ I_1 =-\int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^2\sin x}{\sin x- x\cos x}\,\mathrm dx
= - \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^2}{1-x\cot x}\,\mathrm dx = - J_{21},\tag1$$
where
$$J_{mn} = \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^m}{(1-x\cot x)^n}\,\mathrm dx.\tag2$$
On the other hand,
$$J_{21} = \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^2(1-x\cot x + x\cot x)}{1-x\cot x}\,\mathrm dx = \dfrac{\pi^3}{24} + I_2,$$
where
$$I_2 = \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^3\cot x}{1 - x\cot x}\,\mathrm dx
= \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^3}{\tan x - x}\,\mathrm dx.\tag3$$
Formulas $(3)$ are not suitable for numeric calculations.
But integration by parts is possible,
$$I_2 = \dfrac14\int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{1}{\tan x - x}\,\mathrm dx^4
= \dfrac14\dfrac{x^4}{\tan x-x}\bigg|_{\,0}^{\Large^\pi\hspace{-1pt}/_2}
+ \dfrac14\int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^4(1+\tan^2x -1)}{(\tan x - x)^2}\,\mathrm dx,$$
$$ I_2 = \dfrac14\int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^4}{(1 - x\cot x)^2}\,\mathrm dx = \dfrac14 J_{42},$$
$$I = \dfrac\pi2\ln2 - \dfrac{\pi^3}{24} - \dfrac14 J_{42}.\tag4$$
Formula $(4)$ provides both suitable numeric calculations via Wolfram Alpha by the expression

with the result

and the further building of the series in the elementary functions via the transformations in the form of
$$ J_{42} = \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^4((1 - x\cot x)^2 + 2x\cot x(1 - x\cot x) + x^2\cot^2 x) }{(1 - x\cot x)^2}\,\mathrm dx\\
= \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\left(x^4 + 2\,\dfrac{x^5\cot x}{1-x\cot x} + \dfrac{x^6\cot^2x}{(1 - x\cot x)^2}\right)\,\mathrm dx\\
= \int\limits_0^{\Large^\pi\hspace{-1pt}/_2} x^4\,\mathrm dx
+ \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\left(\dfrac{2x^5\cot x}{1-x\cot x} + \dfrac{x^6\cot^2x}{(1 - x\cot x)^2}\right)\,\mathrm dx,$$
$$J_{42} = \dfrac{\pi^5}{160} + I_3 + I_4,\tag5$$
where
$$I_3 = 2\int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^5\cot x}{1-x\cot x} \,\mathrm dx
= 2\int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^5}{\tan x - x}\,\mathrm dx
= \dfrac13\int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{1}{\tan x - x}\,\mathrm dx^6\\
= \dfrac13\dfrac{x^6}{\tan x-x}\bigg|_{\,0}^{\Large^\pi\hspace{-1pt}/_2}
+ \dfrac13\int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^6(1+\tan^2x -1)}{(\tan x - x)^2}\,\mathrm dx = \dfrac13 J_{62},$$
$$I_4 = \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^6\cot^2x}{(1 - x\cot x)^2}\,\mathrm dx
= \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^6}{(\tan x - x)^2} \,\mathrm dx
= \dfrac17\int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{1}{(\tan x - x)^2} \,\mathrm dx^7\\
= \dfrac27\dfrac{x^7}{(\tan x-x)^3}\bigg|_{\,0}^{\Large^\pi\hspace{-1pt}/_2}
+ \dfrac27\int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^7(1+\tan^2x -1)}{(\tan x - x)^3}\,\mathrm dx
= \dfrac27\int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^7\cot x}{(1 - x\cot x)^3}\,\mathrm dx\\
= \dfrac27\int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^6(1 - (1 - x\cot x))}{(1 - x\cot x)^3}\,\mathrm dx =\dfrac27(J_{63}-J_{62}),$$
Therefore,
$$I = \dfrac\pi2\ln2 - \dfrac{\pi^3}{24} - \dfrac{\pi^5}{640} - \dfrac1{84}J_{62} - \dfrac1{14}J_{63}.\tag6$$
Numeric calculations via Mathcad Alpha by the formula $(6)$
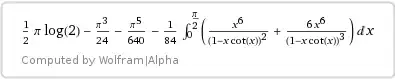
leads to the same result, and this confirms the correctness of the approach.
$\color{brown}{\textbf{Recurrence relations.}}$
For the arbitrary $m,n$
$$ J_{mn} = \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\,(x\cot x + (1-x\cot x))^n \dfrac{x^m}{(1 - x\cot x)^n}\,\mathrm dx
= \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\sum\limits_{k=0}^n\binom nk\dfrac{x^{m+k}\cot^k x}{(1 - x\cot x)^k}\,\mathrm dx
= \dfrac{\pi^{m+1}}{(m+1)2^{m+1}} + \sum\limits_{k=1}^n\dfrac{\dbinom nk}{m+k+1} \int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{\mathrm dx^{m+k+1}}{(\tan x - x)^k}
= \dfrac{\pi^{m+1}}{(m+1)2^{m+1}}\\
+ \sum\limits_{k=1}^n\dfrac{\dbinom nk}{m+k+1} \left(\dfrac{x^{m+k+1}}{(\tan x - x)^{k}}\bigg|_{\,0}^{\Large^\pi\hspace{-1pt}/_2}
+ k\int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^{m+k+1}(1+\tan^2x-1)}{(\tan x-x)^{k+1}}\,\mathrm dx\right)\\
= \dfrac{\pi^{m+1}}{(m+1)2^{m+1}}
+ \sum\limits_{k=1}^n\dfrac{k}{m+k+1} \dbinom nk
\int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^{m+2}(x\cot x)^{k-1}}{(1 -x\cot x)^{k+1}}\,\mathrm dx\\
= \dfrac{\pi^{m+1}}{(m+1)2^{m+1}}
+ \sum\limits_{k=1}^n\dfrac{k}{m+k+1} \dbinom nk
\int\limits_0^{\Large^\pi\hspace{-1pt}/_2}\dfrac{x^{m+2}(1-(1-x\cot x))^{k-1}}{(1 -x\cot x)^{k+1}}\,\mathrm dx\\
= \dfrac{\pi^{m+1}}{(m+1)2^{m+1}}
+ \sum\limits_{k=1}^n\dfrac{k}{m+k+1} \dbinom nk \sum\limits_{j=0}^{k-1}(-1)^{k-1-j}\dbinom{k-1}j J_{m+2,\,j+2},$$
$$J_{mn} = \dfrac{\pi^{m+1}}{(m+1)2^{m+1}}
+ \sum\limits_{j=0}^{n-1} F_{j} J_{m+2,\,j+2},\tag7$$
where
$$F_{j} = \sum\limits_{k=j+1}^n (-1)^{k-1-j} \dfrac{k}{m+k+1}\dbinom nk \dbinom{k-1}j.\tag8 $$
If $(m,n)=(2,1),\ $ then
$$F_{0} = \sum\limits_{k=1}^1 (-1)^{k-1} \dfrac{k}{2+k+1}\dbinom1k \dbinom{k-1}0
=\dfrac14,$$
$$J_{21} = \dfrac{\pi^{3}}{3\cdot2^3} + \sum\limits_{j=0}^0 F_{j} J_{4,\,j+2}
= \dfrac{\pi^{3}}{24} + J_{42}.$$
If $(m,n)=(4,2),\ $ then
$$F_{0} = \sum\limits_{k=1}^2 (-1)^{k-1} \dfrac{k}{4+k+1}\dbinom2k \dbinom{k-1}0
=\dfrac13 - \dfrac27 = \dfrac{1}{21},$$
$$F_{1} = \sum\limits_{k=2}^2 (-1)^{k} \dfrac{k}{4+k+1}\dbinom2k \dbinom{k-1}1
=\dfrac27,$$
$$J_{42} = \dfrac{\pi^{5}}{5\cdot2^5} + \sum\limits_{j=0}^1 F_{j} J_{2,\,j+2}
= \dfrac{\pi^5}{160} + \dfrac1{21}J_{62} + \dfrac27J_{63}.$$
Similarly,
$$J_{62} = \dfrac{\pi^7}{896}+\dfrac1{36}J_{82}+\dfrac29J_{83}\tag9$$
(see also Wolfram Alpha test).
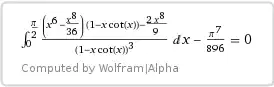
Besides,
$$J_{63} = \dfrac{\pi^7}{896}+\dfrac1{120}J_{82} + \dfrac1{15}J_{83} + \dfrac3{20}J_{84}.\tag{10}$$
$\color{brown}{\textbf{Simple series.}}$
Obtained results are not the best way to get required series of the arbitrary length.
$$\boxed{
\begin{matrix}
I & = & -3.35333726288947201778500718670823032009876022464933939598 \\
\frac\pi2\ln2 & = &1.088793045151801065250344449118806973669291850184643147162 \\
J_{21} & = & 4.442130308041273083035351635930890531086461245854584994170 \\
\frac{\pi^3}{24} & = & 1.291928195012492507311513127795891466759387023578546153922 \\
J_{42} & = & 12.60080845211512230289535403253999625730829688910415536099 \\
\frac{\pi^5}{160} & = & 1.912623029908009082892133187771472540501879416425468690959 \\
J_{62} & = & 9.357325953756236734147158157553707227832359838953032605558 \\
J_{63} & = & 35.84909465209885681432007993043088180418373451454989791084 \\
\frac{\pi^7}{896} & = & 3.370862977429455432493534032446475258836420173320761453966 \\
J_{82} & = & 13.21743446830609099759197972403428192140938899336281280188 \\
J_{83} & = & 25.28690408493225448274231109747825862030555487117486858192 \\
J_{84} & = & 102.2743092725712233044348622015074565154951081384648503713 \\
\end{matrix}}$$
On the other hand, using of the simple Laurent series for the function
$$g(y) = \dfrac{35}{1-y\sqrt{15}\cot y\sqrt{15}} = \dfrac7{y^2}-\sum\limits_{i=0}^\infty c_iy^{2i}\tag{11}$$

gives evidently convergent series
$$J_{21} = \dfrac1{35}\int\limits_0^{\Large^\pi\hspace{-1pt}/_2}
\left(7 - \sum\limits_{i=0}^\infty c_i\left(\dfrac{x^2}{15}\right)^{i+1}\right)\,\mathrm dx,$$
$$J_{21} = \dfrac32\pi - \dfrac3{14}\pi\sum\limits_{i=0}^\infty \dfrac{c_i}{2i+3}\left(\dfrac{\pi^2}{60}\right)^{i+1}\,\mathrm dx,\tag{12}$$
wherein the first $8$ terms provide the accuracy of $8$ decimal digits.