How to solve this integral/better way to approach?

Question

$$\int_{0}^{c} dy \sqrt{\frac{c-1/2y^2+1/3y^3}{1+2y}}$$ where c is a constant. This is coming from trying to find the area $$\int_{U \le c} dq_1dq_2$$ where $$U=\frac{1}{2}(q_1^2+q_2^2)-\frac{1}{3}q_2^3+q_1^2q_2$$ bounded by energy $c=U(q_1,q_2)$.

Answer 1

(Not an answer, just a comment that was too long).

You can prove that the value of the integral is $\frac{c^2}{2\sqrt{6}} + O(c)$ with the following algebraic simplifications. First note that the integral can be written as $$ I = \frac{1}{\sqrt{6}}\int_0^c \sqrt{ (y-1)^2 + \frac{6c-1}{2y+1}} \ dy. $$ It follows that $$I > \frac{1}{\sqrt{6}} \int_0^c (y-1) \ dy = \frac{c(c-2)}{2\sqrt{6}}.$$ Similarly, using the fact that $\sqrt{a+b} < \sqrt{a} + \sqrt{b}$ (which does not quite hold in some regions of the domain but seems to be insignificant for large $c$), we have $$ I < \frac{1}{\sqrt{6}} \int_0^c (y-1) \ dy + \frac{1}{\sqrt{6}}\int_0^c \sqrt{\frac{6c-1}{2y+1}} \ dy = \frac{c^2}{2\sqrt{6}} + O(c).$$ Thus we can conclude that $I = \frac{c^2}{2\sqrt{6}} + O(c).$ I think what could possibly help you is the following:

• If you want just a numerical answer, the function you are integrating is very smooth and convex so getting high precision values is doable.
• If you want a more accurate answer, you need to specify what regions of $c$ you are interested in. My answer holds for $c \rightarrow \infty$ but there are certainly more accurate answers for other cases such as $c << 1$.

Answer 2

$$\color{brown}{\textbf{Edition of 02.12.2018}}$$

HINT

The issue task is the task about the area under not convex figure.

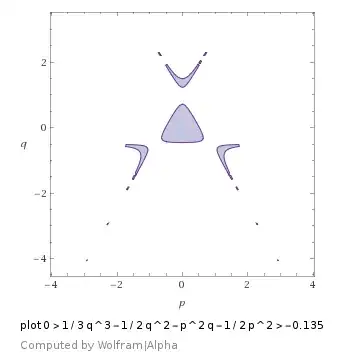
In particular, for $C=0.135$ the graph is

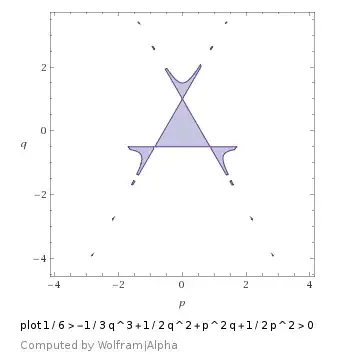
for $C=\frac16$ the graph is

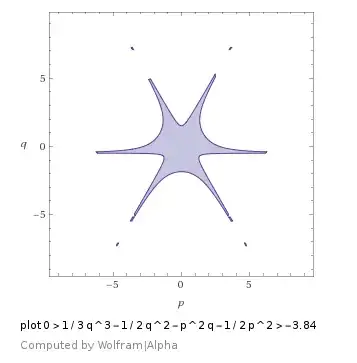
and for $C=3.84$ the graph is

These figures show, that the proposed integral can't calculate the area correctly, and it can be suitable to calculate the area in polar coordinates.

Let $$q_1=r\cos \varphi, \quad q_2=r \sin\varphi,$$ then $$U(r,\varphi) = \dfrac13r^3\sin 3\varphi+\dfrac12r^2.\tag1$$ Taking in account the properties of the sine function, it is sufficiently to consider $U(r,\varphi)$ at the interval $$\varphi\in\left(\frac\pi6,\frac\pi2\right).$$ The bounds determines by the system of inequalities \begin{cases} \dfrac13r^3\sin 3\varphi+\dfrac12r^2 > 0\\ \dfrac13r^3\sin 3\varphi+\dfrac12r^2 < C.\tag2 \end{cases} The first inequality has the solution $$\begin{cases} r\in(0,\infty),\quad \text{if}\quad \varphi\in\left(\dfrac\pi6,\dfrac\pi3\right)\\ r\in\left(0,-\dfrac3{2\sin3\varphi}\right),\quad \text{if}\quad \varphi\in\left(\dfrac\pi3,\dfrac\pi2\right) \end{cases}\tag3$$ Factor $\dfrac4{Cr^3}$ allows to present the second inequality in the form of $$\dfrac{4}{r^3} - \dfrac2{Cr} > \dfrac{4\sin3\varphi}{3C},$$ or $$4\left(\dfrac ar\right)^3-3\dfrac{a}r > p,\tag4$$ where $$a=\sqrt{\dfrac{3C}2},\quad p=2a\sin3\varphi.\tag5$$ $\textbf{If p < 1,}$ then can be used representation $$\cos\left(3\arccos\left(\dfrac ar\right)\right) > p.$$ Then $$\dfrac ar\in \begin{cases} [0,1],\quad\text{if}\quad p\in[-\infty,-1)\\ \left[\cos\left(\dfrac13\arccos p\right),\infty \right]\bigcup\left[0,\cos\left(\dfrac{2\pi}3-\dfrac13\arccos p\right)\right],\quad\text{if}\quad p\in[-1,1] \end{cases} $$ (see also Wolfram Alpha)

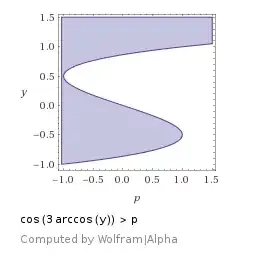$$r\in \begin{cases} [a,\infty],\text{ if }p\in[-\infty,-1)\\ \left[0,\dfrac a{\cos\left(\dfrac13\arccos p\right)}\right] \bigcup\left[\dfrac a{\cos\left(\dfrac{2\pi}3-\dfrac13\arccos p\right)},\infty\right],\text{ if } p\in[-1,1], \end{cases}\tag6 $$ $\textbf{If p > 1,}$ then can be used representation $$\cosh\left(3\cosh^{-1}\left(\dfrac ar\right)\right) > p,$$ $$ r < \dfrac a{\cosh\left(\dfrac13\cosh^{-1}p\right)},$$ wherein $$\cosh^{-1}x = \log(x+\sqrt{x^2-1}),$$ $$\cosh\left(\dfrac13\cosh^{-1}x\right)=\dfrac12\left(\sqrt[3]{x+\sqrt{x^2-1}}+\dfrac1{\sqrt[3]{x+\sqrt{x^2-1}}}\right).$$ So $$r < \dfrac {2a}{\sqrt[3]{p+\sqrt{p^2-1}}+\sqrt[3]{p-\sqrt{p^2-1}}}.\tag7$$ Besides, $r\ge0.$ Let us consider two examples.

$$\textbf{Example C=0.135, a=0.45}$$ The control points are $$p\left(\dfrac\pi6\right)=0.9,\quad p\left(\dfrac\pi3\right)=0,\quad p\left(\dfrac{2\pi}5\right)=-0.593083,\quad p\left(\dfrac\pi2\right)=-0.9,$$ $$r\left(\dfrac\pi6\right)\in(0,0.455304),\quad r\left(\dfrac\pi3\right)\in(0,0.519615),\quad r\left(\dfrac{2\pi}5\right)\in(0,0.519615)\cup(2.43582,2.55195),\quad r\left(\dfrac\pi2\right)\in((0,0.721023)\cup(1.23406,1.5)).$$

System $(2)$ has solutions $$\left[\begin{align} r\in\left(0,\dfrac {0.45}{\cos\left(\dfrac13\arccos (0.9\sin3\varphi)\right)}\right),\quad \text{if}\quad \varphi\in\left(\dfrac\pi6,\dfrac\pi2\right)\\ r\in\left(\dfrac {0.45}{\cos\left(\dfrac{2\pi}3-\dfrac13\arccos(0.9\sin3\varphi) \right)},-\dfrac3{2\sin3\varphi}\right),\quad \text{if}\quad \varphi\in\left(\dfrac\pi3,\dfrac\pi2\right) \end{align}\right.\tag8$$ The obtained results correspond with the first graph.

$$\textbf{Example C=3.84, a=2.4}$$ The control points are $$p\left(\dfrac\pi6\right)=4.8,\quad p\left(\dfrac\pi3-\dfrac13\arcsin\dfrac5{24}\right)=1,\quad p\left(\dfrac\pi3-\dfrac13\arcsin 0.2\right)=0.96,\quad p\left(\dfrac\pi3\right)=0,\quad p\left(\dfrac\pi3+\dfrac13\arcsin 0.2\right)=-0.96,\quad p\left(\dfrac\pi3+\dfrac13\arcsin\dfrac5{24}\right)=-1,\quad p\left(\dfrac{2\pi}5\right)=-2.82137, \quad p\left(\dfrac\pi2\right)=-4.8,$$ $$r\left(\dfrac\pi6\right)\in(0,1.85345),\quad r\left(\dfrac\pi3-\dfrac13\arcsin\dfrac5{24}\right)=(0,2.4),\quad r\left(\dfrac\pi3-\dfrac13\arcsin0.2\right)=(0,2.41078),\quad r\left(\dfrac\pi3\right)\in(0,2.77128),\quad r\left(\dfrac\pi3+\dfrac13\arcsin0.2\right)=(0,4.14103)\cup(5.76975,7.5),\quad r\left(\dfrac\pi3+\dfrac13\arcsin\dfrac5{24}\right)=(0,7.2),\quad r\left(\dfrac{2\pi}5\right)\in(0,2.55195),\quad r\left(\dfrac\pi2\right)\in(0,1.5).$$

System $(2)$ has solutions $$\begin{cases} r\in\left(0,\dfrac {4.8}{\sqrt[3]{4.8\sin3\varphi+\sqrt{(4.8\sin3\varphi)^2-1}}+\sqrt[3]{4.8\sin3\varphi-\sqrt{(4.8\sin3\varphi)^2-1}}}\right),\quad \text{if}\quad \varphi\in\left(\dfrac\pi6,\dfrac\pi3-\dfrac13\arcsin\dfrac5{24}\right)\\ r\in\left(0,\dfrac {2.4}{\cos\left(\dfrac13\arccos (4.8\sin3\varphi)\right)}\right),\quad \text{if}\quad \varphi\in\left(\dfrac\pi3-\dfrac13\arcsin\dfrac5{24},\dfrac\pi3\right)\\ r\in\left(0,\dfrac {2.4}{\cos\left(\dfrac13\arccos (4.8\sin3\varphi)\right)}\right)\bigcup\left(\dfrac {2.4}{\cos\left(\dfrac{2\pi}3-\dfrac13\arccos(4.8\sin3\varphi) \right)},-\dfrac3{2\sin3\varphi}\right),\quad \text{if}\quad \varphi\in\left(\dfrac\pi3,\dfrac\pi3+\dfrac13\arcsin\dfrac5{24}\right)\\ r\in\left(0,-\dfrac3{2\sin3\varphi}\right),\quad \text{if}\quad \varphi\in\left(\dfrac\pi3+\dfrac13\arcsin\dfrac5{24},\dfrac\pi2\right) \end{cases}\tag9$$ The obtained results correspond with the third graph.

$\textbf{Finding the area}$

The area of figure in the polar coordinates equals to

$$S=6\cdot\dfrac12\int\limits_{\pi/6}^{\pi/2}r^2(\varphi)\,\mathrm d\varphi.$$

In particular, for $C=0.135$

$$S=6\cdot\dfrac12\int\limits_{\pi/6}^{\pi/2}\dfrac {0.45^2}{\cos^2\left(\dfrac13\arccos (0.9\sin3\varphi)\right)}\,\mathrm d\varphi +6\cdot\dfrac12\int\limits_{\pi/3}^{\pi/2}\left(\dfrac{9}{4\sin^2(3\varphi)} - \dfrac {0.45^2}{\cos^2\left(\dfrac{2\pi}3-\dfrac13\arccos (0.9\sin3\varphi)\right)}\right)\,\mathrm d\varphi \approx 0.968088 + 0.968088 = \mathbf{1.937376}$$ (see also Wolfram Alpha for the first integral and for the second one)

Answer 3

The Appell-Lauricella function is defined by the series $$ F[\{a,c\};\{b_1,b_2,\dots,b_n\};\{x_1,x_2,\ldots,x_n\}]:= $$ $$ =\sum_{i_1,i_2,\ldots,i_n\geq 0}\frac{(a)_{i_1+i_2+\ldots+i_n}(b_1)_{i_1}(b_2)_{i_2}\ldots(b_n)_{i_n}}{(c)_{i_1+i_2+\ldots+i_n}i_1!i_2!\ldots i_n!}x_1^{i_1}x_2^{i_2}\ldots x_n^{i_n}, $$ where $n\geq2$, $a,c,b_1,b_2,\ldots,b_n\in\textbf{C}$ and $|x_1|<1,|x_2|<1,\ldots,|x_n|<1$.

Then holds the following

THEOREM. For $Re(c)>Re(a)>0$ and $|x_1|<1,|x_2|<1,\ldots,|x_n|<1$, we have $$ F[\{a,c\};\{b_1,b_2,\dots,b_n\};\{x_1,x_2,\ldots,x_n\}]= $$ $$ =\frac{\Gamma(c)}{\Gamma(a)\Gamma(c-a)}\int^{1}_{0}t^{a-1}(1-t)^{c-a-1}(1-x_1t)^{-b_1}(1-x_2t)^{-b_2}\ldots (1-x_nt)^{-b_n}dt. $$

Using the above theorem I will prove that

$$ \int^{c}_{0}\sqrt{\frac{c-y^2/2+y^3/3}{1+2y}}dy= \frac{c\sqrt{4-l}}{2\sqrt{6}}|l-1|\times $$ $$ \times F\left[\{1,2\};\{\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\};\{-2c,\frac{2c}{l-1},\frac{4c}{4-l-\sqrt{3}\sqrt{(4-l)l}},\frac{4c}{4-l+\sqrt{3}\sqrt{(4-l)l}}\}\right], $$ where $c=\frac{1}{24}(4-9l+6l^2-l^3)$.

For to prove the above evaluation make the change of variable $y\rightarrow -y$ to get $$ \int^{c}_{0}\sqrt{\frac{c-y^2/2+y^3/3}{2y+1}}dy=i\int^{-c}_{0}\sqrt{\frac{y^2/2+y^3/3-c}{-2y+1}}dy, $$ then $y\rightarrow \frac{1-w}{2}$ to get $$ i\int^{-c}_{0}\sqrt{\frac{y^2/2+y^3/3-c}{-2y+1}}dy=\frac{\sqrt{c}}{4\sqrt{6}}\int^{2c+1}_{1}\sqrt{\frac{24+1/c(w-4)(w-1)^2}{w}}dw. $$ Now if $c=\frac{1}{24}(4-9l+6l^2-l^3)$ we can write $$ 24+(-4+w)(-1+w)^2/c=\frac{24(l-w)(9-6l+l^2-6w+lw+w^2)}{(l-4)(l-1)^2}. $$ Hence we can write the last integral in the form of theorem and use it to get the result, which is the Appell-Lauricella function.