$n$ be the smallest positive integer such that $1+ \frac{1}{2} + \frac{1}{3} + \frac {1}{4}+\cdots \geq 4$.

Question

$n$ be the smallest positive integer such that $1+ \frac{1}{2} + \frac{1}{3} +\frac14+\cdots \geq 4$.

My Attempt : I can show that $ \log(n+1) \leq 1+ \frac{1}{2} + \frac{1}{3} + \frac {1}{4} +\cdots+ \frac {1}{n}$. And by using this inequality I can say that the smallest number will be less than $54$. But I can not find the smallest number.

Can anyone please help me by giving some hints.

Maybe do an integral approximation. Maybe that is already what you tried? It is difficult to say because you don't explain where the log comes from. — mathreadler, Dec 11 '19 at 11:13
The sum is the area under steps of width 1 and height $1/k$. Log is the area under $y=1/x$, which is slightly below the steps. Do a few steps first then $y=1/x$ the rest of the way. That is a closer estimate. — Empy2, Dec 11 '19 at 11:24
@Paul Frost: I had no idea it would be that weak of a result for the OP's question! I'm pretty busy with other stuff now, and so I didn't take any time to see how helpful that approximation could be. I have an old manuscript that I suspect gives (with proof) a sufficiently accurate approximation, but unfortunately Math Forum discussion group links aren't working (where it's at; I've cited it several times in the past 8 or so years in Stack Exchange, in fact). Maybe this 22 March 2001 sci.math post of mine will be of use. — Dave L. Renfro, Dec 11 '19 at 12:02
@DaveL.Renfro There are certainly much better bounds than $\ln(n+1) < H_n < \ln(n)+1$, but the effort to prove them is certainly much bigger than to answer to OP's question by a simple calculation. The (poor) upper bound $n \le 53$ shows that this can be done easily. Finding the smallest $n$ such that $H_n \ge M$ for a big $M$ doesn't work by calculations, so your approach is of course much better for the general case. By the way, are there good approximations for small $n$? — Paul Frost, Dec 11 '19 at 14:51
I'd like to know where the problem comes from. Were you asked to write a program to calculate $n$? Or is it your own curiosity that created the question? — Calum Gilhooley, Dec 11 '19 at 15:47
@Paul Frost: For small values of $n$ you can use many terms of the standard series obtained from the Euler–Maclaurin summation formula. See Simple proof of showing the Harmonic number $H_n = \Theta (\log n)$ and this google search. I notice that $\ln n + \gamma + \frac{1}{2n} - \frac{1}{8n^2} < H_n < \ln n + \gamma + \frac{1}{2n}$ mentioned in the sci.math post I cited can be used (with a good enough value for $\gamma)$ to show that $H_{30} < 4$ and $H_{31} > 4.$ — Dave L. Renfro, Dec 11 '19 at 16:51
The probable source of the problem is 9) on page 9 of this PDF file, a 2017 paper from the KVPY exam (Indian Institute of Science). The multiple-choice question reads:
Let $n$ be the smallest positive integer such that $$ 1+\frac12+\frac13+\cdots+\frac1n\geq4. $$ Which one of the following statements is true? A) $20<n\leq60$ B) $60<n\leq80$ C) $80<n\leq100$ D) $100<n\leq120$.

See Harmonic series sum approximation

of which the present question is, sadly, a duplicate. — Calum Gilhooley, Dec 11 '19 at 19:50
Another duplicate: Find the least Positive Integer Satisfying $1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n} \ge 4$. — Calum Gilhooley, Dec 11 '19 at 21:00

Ty Jensen · Answer 1 · 2019-12-11T20:04:52.920

4

Since I am receiving a lot of flack for my poor use of inequalities, I will try to improve my method. First, note that you are analyzing the Harmonic Series $H_n$ and: $$H_n \approx ln(n)+\gamma$$ However, $$H_n < ln(n) +\gamma$$ For all $n$. Luckily, $$H_n \approx ln(n) +\gamma - \frac{1}{n}$$ and $$H_n > ln(n) +\gamma - \frac{1}{n}$$ for all $n$, so we have $$ln(n) +\gamma + \frac{1}{n}<H_n<ln(n) +\gamma$$ If you want to see just how good these approximations are, look at them all graphed: https://www.desmos.com/calculator/a5ibmgvsdy

We would like to show for which the smalles value of $n$, $H_n \leq 4$ so lets solve both sides of the equality for $4$. $$4<ln(n) + \gamma$$ $$4- \gamma < ln(n)$$ $$e^{4-\gamma}<n$$ $$30.6546491214 \lessapprox n$$ Now for the other side $$ln(n) +\gamma - \frac{1}{n}<4$$ $$ln(n)-\frac{1}{n}<4-\gamma$$ And after analyzing the graph of $ln(n) + \frac{1}{n}$ (since $n$ isn't separable) $$n \lessapprox 31.6$$ So finally we have $$30.6546491214\lessapprox n \lessapprox 31.6$$ Therefore if $n$ is an integer, we can approximate $$H_{31} \geq 4$$

I put this into Desmos for you as well so you can verify it is true: https://www.desmos.com/calculator/ttjyfn6ph3

edited Dec 11 '19 at 20:04

answered Dec 11 '19 at 11:16

Ty Jensen

1,516

2

How do you switch from $\approx$ to $\ge$ ? – Dec 11 '19 at 13:46
@YvesDaoust well I took the ceiling of the answer anyways, but I'll go ahead and fix it if it bothers you – Ty Jensen Dec 11 '19 at 13:50
2

In fact, $\ln(n)+\gamma<H_n$ for all $n$. Your $ \gtrapprox$ does not hold. We even have $\lceil\ln(11)+\gamma\rceil<\lceil H_{11}\rceil$. – Dec 11 '19 at 13:50
Still $H_{31} \approx ln(31)+ \gamma$ is a good enough approximation in the context of this problem, hence the correct answer. But I will add another fix to better this I guess – Ty Jensen Dec 11 '19 at 13:54
2

That doesn't allow you to write wrong inequalities. And as you are looking for a near-integer, the approximation has high chances to be off. – Dec 11 '19 at 13:55
Okay, so would you like me to add $\frac{1}{n}$ to the approximation? – Ty Jensen Dec 11 '19 at 14:12
3

Do what you want but don't leave the wrong inequalities. – Dec 11 '19 at 14:30
1

As Yves Daoust remarked, we have $H_n > \ln(n) +\gamma$. Instead of $H_n \ge 4$ you look when $\ln(n) +\gamma \ge 4$ which gives $n \ge 30.6546491214$. Thus $H_{31} \ge 4$, but $n = 31$ may not be the smallest integer. – Paul Frost Dec 11 '19 at 15:36
@PaulFrost Thank you Paul, that makes sense! I think I have cleaned everything up now. – Ty Jensen Dec 11 '19 at 15:44
2

Grrrr, you still leave the wrong inequality, despite warnings by two guys ! – Dec 11 '19 at 18:59
Sorry, just got back from class, how does the new solution look? – Ty Jensen Dec 11 '19 at 20:05

mathreadler · Answer 2 · 2019-12-11T12:36:19.323

2

Not assuming as much knowledge about the Harmonic series as the other answers, we can also do an integral approximation by Riemann sum.

Since $f(x) = 1/x$ is monotonic decreasing

$$\sum_{k=1}^N 1/k \approx 1+\int_{1}^{N}{\frac{1}x dx} = 1+\left[\log(x)\right]_1^N = \log(N)-\log(1)+1 = 4$$

But because of systematic underestimation due to the monotonic nature of our log function we might as well choose one displaced by one step and get systematic overestimation. The mean value of these will be $$(\exp(3)+\exp(3+1))/2 \approx 37$$

But the nature of this mean involving exponential functions, a geometric mean might be more suitable than an arithmetic mean:

$$\sqrt[2]{e^3 \cdot e^4} = e^{3.5}\approx 33$$

The real value appears to be $31$ or $32$.

edited Dec 11 '19 at 12:36

answered Dec 11 '19 at 11:24

mathreadler

25,824

I can not understand this --- $$\sum_{k=1}^N 1/k \approx 1+\int_{1}^{N}{\frac{1}x dx} = 1+\left[\log(1+x)\right]_1^N = log(N+1)-log(2)+1 = 4$$ – cmi Dec 11 '19 at 11:40
@cmi I added a link to Riemann sum technique. – mathreadler Dec 11 '19 at 11:43
I know Riemann sum but I can not connect this with the Riemann sum.. I think You have made some mistake...@mathreadler – cmi Dec 11 '19 at 11:56
Some problem in the integration as well.@mathreadler – cmi Dec 11 '19 at 12:18
Of course you can. This is first calculus class level stuff. – mathreadler Dec 11 '19 at 12:21
Maybe you mean I had some arithmetic errors, that is true. I think I fixed them now. – mathreadler Dec 11 '19 at 12:39

score 2 · Answer 3 · answered Dec 11 '19 at 13:22

We have $$x-1<\lfloor x\rfloor\le x$$ and $$\frac1x\le\frac1{\lfloor x\rfloor}<\frac1{x-1}.$$

Now integrating between $2$ and $n+1$, and adding $1$,

$$1+\log\frac{n+1}2\le\sum_{k=1}^n\frac 1k<1+\log n.$$

The lower and upper bounds equal $4$ for $n=41.17$ and $n=20.09$ and the desired solution will lie in that range.

We can narrow that range by computing more terms explicitly

$$1+\frac12+\frac13+\frac14+\frac15+\log\frac{n+1}6\le\sum_{k=1}^n\frac 1k<1+\frac12+\frac13+\frac14+\frac15+\log\frac n5,$$gives $32.40$ and $27.83$.

Claude Leibovici · Answer 4 · 2019-12-12T03:36:03.360

$$\sum_{i=1}^n \frac 1i=H_n$$ For large values of $n$ $$H_n=\gamma +\log \left({n}\right)+\frac{1}{2 n}+O\left(\frac{1}{n^2}\right)$$ So, using the first term only $$H_n=k \implies \gamma +\log \left({n}\right) = k \implies n_{(1)} = e^{k-\gamma }$$

Using the first and second term of the expansion, the solution of the equation is given in terms of Lambert function $$H_n=k \implies \gamma +\log \left({n}\right)+\frac 1 {2n} = k \implies n_{(2)} =-\frac{1}{2 W\left(-\frac{1}{2}e^{\gamma -k}\right)}$$

Some results for a few values of integer $k$'s $$\left( \begin{array}{ccccc} k & n_{(1)}& n_{(2)} & \text{exact} & H_{n_{(2)}}-k \\ 2 & 4.14866 & 3.6124 & 3.63868 & -6.34\times 10^{-3} \\ 3 & 11.2772 & 10.7654 & 10.7735 & -7.18 \times 10^{-4}\\ 4 & 30.6546 & 30.1505 & 30.1533 & -9.17 \times 10^{-5}\\ 5 & 83.328 & 82.8265 & 82.8275 & -1.21 \times 10^{-5}\\ 6 & 226.509 & 226.008 & 226.009 & -1.63\times 10^{-6}\\ 7 & 615.715 & 615.215 & 615.215 & -2.20 \times 10^{-7}\\ 8 & 1673.69 & 1673.19 & 1673.19 & -2.98 \times 10^{-8}\\ 9 & 4549.55 & 4549.05 & 4549.05 & -4.03 \times 10^{-9}\\ 10 & 12367.0 & 12366.5 & 12366.5 & -5.45\times 10^{-10} \end{array} \right)$$

Hi Claude. Notice that $\log(n)+\gamma<H_n$ so that $n\ge e^{4-\gamma}$ could be wrong (by chance, it is not). — , Dec 11 '19 at 14:02
@YvesDaoust. We can do much better at the price of Lambert function which leads to $30+\epsilon$. But you are right. Cheers. — Claude Leibovici, Dec 11 '19 at 17:43

Paul Frost · Answer 5 · 2019-12-11T14:11:52.303

1

There are good approximations as shown by the previous answers. Doing it intelligently you get very good estimates. However, it seems to me that the exact value of $n$ can only be determined by explicit calculations. I used Excel:

$\quad$

Here is the complete table up to $n = 32$. Note that Excel uses $8$ decimals, thus the rounding error in these calculations does not affect our result $n = 31$.

edited Dec 11 '19 at 14:11

answered Dec 11 '19 at 12:58

Paul Frost

76,394
12
43
125

Calum Gilhooley · Answer 6 · 2019-12-12T11:41:05.797

According to Harmonic number - Wikipedia, $$ \gamma = \lim_{n\to\infty} \left(H_n - \ln\left(n + \frac12\right)\right) $$ converges more quickly than $$ \gamma = \lim_{n\to\infty}(H_n - \ln(n)). $$ Indeed, in the present case, $$ e^{4 - \gamma} - \frac12 \bumpeq 30.154649 $$ zeroes in on the answer pretty well.

Harmonic Number -- from Wolfram MathWorld gives more detail: $$ \frac1{24(n+1)^2} < H_n - \ln\left(n + \frac12\right) - \gamma < \frac1{24n^2}. $$ These inequalities suffice to determine $n$ exactly, because \begin{align*} H_{30} & < \ln\left(30 + \frac12\right) + \gamma + \frac1{21600} \bumpeq 3.994989, \\ H_{31} & > \ln\left(31 + \frac12\right) + \gamma + \frac1{24576} \bumpeq 4.027244, \end{align*} whence $n = 31.$

The references given in the MathWorld article are:

DeTemple, D. W. "The Non-Integer Property of Sums of Reciprocals of Consecutive Integers." Math. Gaz. 75, 193-194, 1991.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.

Addendum

There are other inequalities that can be used to determine $n$ exactly.

Some are discussed in these books and papers:

B. Berndt, Ramanujan's Notebooks, Volume 5, Springer, New York, 1998.
T. J. l'A. Bromwich, An Introduction to the Theory of Infinite Series, Chelsea, New York, 1991.
E. Cesàro, "Sur la serie harmonique", Nouv. Ann. (3) IV (1885), 295-296.
A. Lodge, "An approximate expression for the value of $1+\frac12+\frac13+\cdots+\frac1r$", Messenger of Mathematics 30 (1904), 103-107.
Mark B. Villarino, "Ramanujan's Approximation to the $n$th Partial Sum of the Harmonic Series" (2004), arXiv:math/0402354 [math.CA].

The simplest of these results is Villarino's Corollary 3, which is originally due to Cesàro ("By the way, this was two years before Ramanujan was born!"), and is given as exercise no. 18 on page 460 of Bromwich's book: $$ H_n = \frac12\ln(2m) + \gamma + \frac{c_n}{12m}, \text{ where } m = \frac{n(n+1)}2 \text{ and } 0 < c_n < 1. $$ This gives: \begin{align*} H_{30} & < 3.99498717, \\ H_{31} & > 4.02707722. \end{align*} For comparison, the exact values are: \begin{align*} H_{30} = 4 \times \frac{9304682830147}{9316358251200} & \bumpeq 3.99498713, \\ H_{31} = 4 \times \frac{290774257297357}{288807105787200} & \bumpeq 4.02724520. \end{align*}

nice and exhaustive answer (+1) – G Cab Dec 11 '19 at 17:01 — G Cab, Dec 11 '19 at 17:01

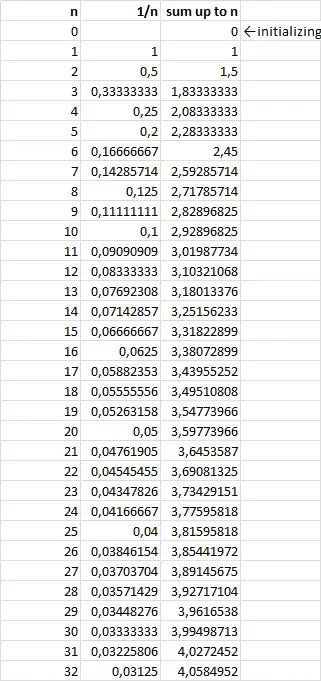
$n$ be the smallest positive integer such that $1+ \frac{1}{2} + \frac{1}{3} + \frac {1}{4}+\cdots \geq 4$.

6 Answers6

Addendum