It is known that F(x) is the generating function of the counting sequence of connected simple graphs with N vertices is given by:
$F(x) = x + x^2 + 2x^3 + 6x^4 + 21x^5 + 112x^6 + ...$
where the total number of connected graphs of $n$ vertices is obtained by the coefficient corresponding to $x^n$.
The question here is: How to find the series (or formula) to get the counting of connected simple graphs with $n$ vertices of maximum degree up to $P$? (generalizing with at least $1$ vertice with maximum degree equal to $P$)
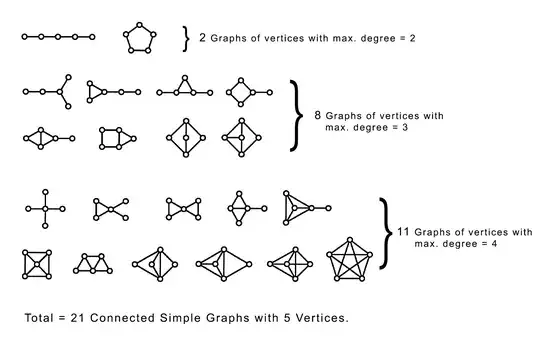
For example, for $n = 5$ with $P=3$, we have $8$ connected graphs with at least $1$ vertice with maximum degree equal to $3$, and for $n = 5$ with $P=4$, we have $11$ connected graphs with at least $1$ vertice with maximum degree equal to $4$, as shown the degree distribution in the illustration below:
Follows a table of the count of the first groups of graphs according to the number of vertices and the maximum degree:
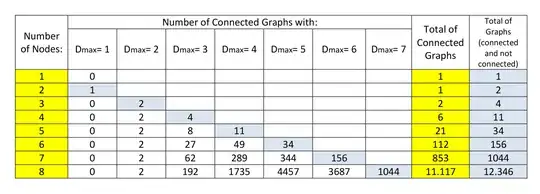My question in brief is to determine the number of connected graphs with max. degree $P$ for a given number of Nodes $n$.
OBS: Do not get confused! the question does not include Disconnected Graphs, Digraphs, Labeled Graphs, number of cubic or quartic graphs!
Anyone know a solution to this intriguing problem? help me!
Note:
F(x) is the generating function of the counting sequence of connected structures, then the corresponding generating function G(x) of the counting sequence of all structures is given by:
$$G(x) = exp \sum_{k>=1} F(x^k)/k = \sum_{i=0} b_i x^k$$
Applying a variant of the Mobius inversion to equation above, it is possible to express F(x) in terms of G(x):
$$F(x) = exp \sum_{k>=1} [\mu(x)/k]log G(x^k) = \sum_{i=0} a_i x^k$$
Where $\mu$ stands for the Mobius function.
Let $a_n$ be the number of connected graphs on $n$ vertices and $b_n$ the number of all graphs on $n$ vertices. Then:
$F(x) = x + x^2 + 2x^3 + 6x^4 + 21x^5 + 112x^6 + 853x^7 + ...$
and
$G(x) = 1 + x + 2x^2 + 4x^3 + 11x^4 + 34x^5 + 156x^6 + ...$
I saw this on "Counting Disconnected Structures: Chemical Trees, Fullerenes, I-graphs" on the link: https://hrcak.srce.hr/file/4232 but I did not understand how I can use it in favor of my problem.
An observation:
If $T(n)$ represents the total of connected graphs of $n$ nodes and $D_p(n)$ represents the total of connected sub-graphs group with max. degree $P$, and knowing that $P_{max} = (n-1)$, we can write: $$ T(n) = D_1(n) + D_2(n) + D_3(n) + ... + D_{n-1}(n)$$
For $n>2$, we know that $D_1(n) = 0$ and $D_2(n) = 2$, so we have to: $$T(n) = 2 + D_3(n) + ... + D_{n-1}(n)$$
Note also that $D_{n-1}$ is obtained by the coefficient of $x^{n-1}$ of $G(x)$.
But how to calculate $D_p(n)$?
OBS: Another way to attack the problem I posted on the link About counting the number of graphs by the maximum Degree $D$.
