This is another way of attacking the problem that I posted on the link: What is the number of connected graphs with $n$ vertices of max. degree up to $P$? Leaving $F(x) = x + x^2 + 2x^3 + 6x^4 + 21x^5 + ...$
I noticed that there are no definitive studies in Graph Theory about counting graphs by degrees (for the maximum degree for example). There are counts of total graphs by the number of nodes, by the number of edges, and analyzes on regular graphs and sequences of degrees.
An example, by the link Enumeration of Graphs with given Degree Sequence, is the asymptotic formula for the number $G_{d,n}$ of d-regular graphs on $n$ vertices with given degree sequence $d = (d,...,d)$:
$$G_{d,n} \sim \frac{(dn)!e^{-(d^2-1)/4}}{(dn/2)!2^{dn/2} \prod d_i!}$$
However, I found the sequence in OEIS: A243393,that represents the total of graphs with maximum degree up to 3. To my surprise there is no closed formula for the sequence!
There does not seem to be an analytical formula for this problem, although it is early and unlikely to state this, as I have seen much more complex problems in mathematics be solved in a majestic way.
Another way to tackle the problem would be experimental, and here's my question: Is there an efficient method to find an approximate function of the curve that represents the sequence based on the given values?
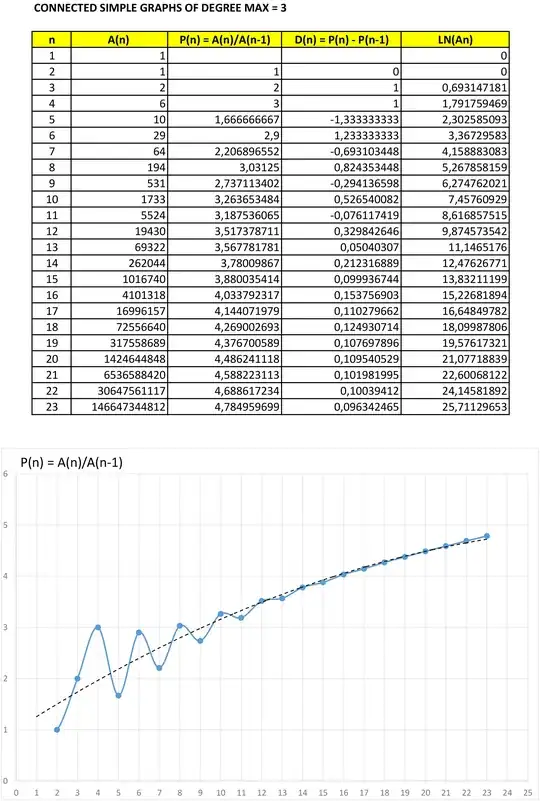
Below is a table containing the total number of connected simple graphs ($A_n$) with a maximum degree up to 3, and some relations between the values, represented by graphics:
Note in the first graph that the function $P(n)$ oscillates around a smooth curve, with a larger oscillation for small $n$. If the function $P(n)$ was estimated, we could obtain:
$$A(n) \approx \prod_{i=2}^n P(i)$$
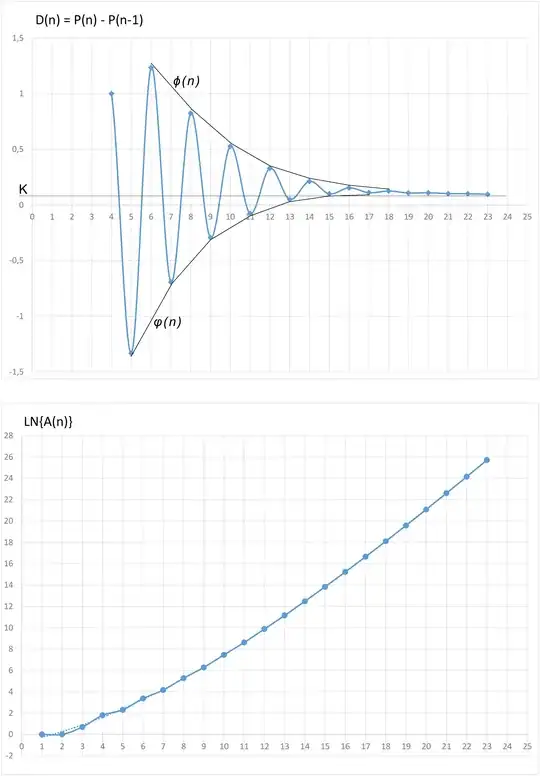
Note in the second graph that the difference $D(n) = P(n)-P(n-1)$ seems to oscillate around a constant $K$. We would have $\lim \limits_{n \to \infty} D_n = K$ ? It seems that the upper and lower delimiting curves $\Phi(n)$ and $\phi(n)$ behave as positive and negative exponentials.
See also in third graph that $Ln(A_n)$ seems to behave as a smooth exponential. Like this?
$$ A(n) \approx e^{e^{an + b}+ c} + d$$
Anyway, there seem to be many ways to try to approximate the function and many other relationships could be observed. What would be a good and efficient method?
Could we perhaps find an asymptote for some relationship? We have $23$ computed values here, would that be little for us to make an analysis for generalization? Is there a method to find an approximate formula (function), even for small values of n?