Patterns of the zeros of the Faulhaber polynomials (modified)

Question

Faulhaber polynomial of order $p \in \Bbb{N}$ is defined as the unique polynomial of degree $p+1$ satisfying

$$ S_{p}(n) = \sum_{k=1}^{n} k^p $$

for $n = 1, 2, 3, \cdots$. For example,

\begin{align*} S_0(x) &= x, \\ S_1(x) &= \frac{x(x+1)}{2}, \\ S_2(x) &= \frac{x(x+1)(2x+1)}{6}, \\ S_3(x) &= \frac{x^2 (x+1)^2}{4}. \end{align*}

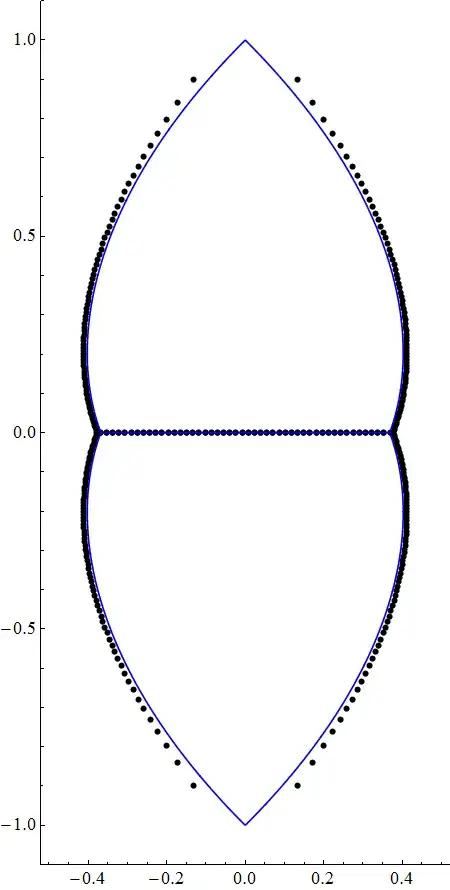
In order to grasp some intuition on the partial decomposition of $1/S_p (x)$, I tried plotting the complex zeros of $S_p (x)$. The following graphics shows the distribution of the zeros of $S_{800}(x)$.

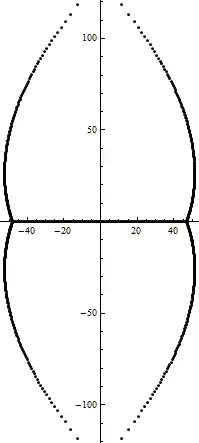
(The precision of the calculated zeros $z_j$ of $S_{800}(z)$ above satisfy $|f(z_j)| \leq 10^{-300}$.)

It turns out that they exhibits a very neat, yet still a strange pattern as seen above.

So far I have never heard of the topic related to this pattern, and I want to know (out of curiosity) if there are some results concerning the pattern of zeros of $S_p(x)$.

Answer 1

First it appears that the zeros are symmetric about the line $x=-1/2$, and indeed the polynomials

$$ F_p(z) = S_p(z-1/2) $$

appear to have only even or only odd powers of $z$.

It seems that the zeros not on the real axis grow on the order of $p/(2\pi)$. Numerically they have the same limiting behavior as the zeros of the partial sums of the sine and cosine series (see this paper [PDF]) as well as the partial sums of the Bessel functions (see this preprint).

Below is a plot of the zeros of $F_p\left(\frac{p}{2\pi}z\right)$ for $p=400$, along with the modified Szegő curve

$$ \begin{align} &\left\{z \in \mathbb{C} \,\colon \Im(z) \geq 0,\,\,\, |z| \leq 1, \,\,\,\text{and}\,\,\, \left|ze^{1+iz}\right| = 1 \right\} \\ &\qquad \cup \,\left\{z \in \mathbb{C} \,\colon \Im(z) \leq 0,\,\,\, |z| \leq 1, \,\,\,\text{and}\,\,\, \left|ze^{1-iz}\right| = 1 \right\} \\ &\qquad \cup \,\left\{x \in \mathbb{R} \,\colon -1/e \leq x \leq 1/e \right\} \end{align} $$

in blue.

There is possibly a connection to the zeros of the Bernoulli polynomials $B_p(x)$ as a result of the fact that

$$ S_p(z) = \frac{B_{p+1}(z+1) - B_{p+1}(0)}{p+1}. $$

You may wish to take a look at Karl Dilcher's memoir Zeros of Bernoulli, Generalized Bernoulli, and Euler Polynomials and this paper by John Mangual.

Answer 2

As an addendum to Antonio Vargas's answer, let's prove that the roots of $S_p$ are indeed symmetrically distributed around $-1/2$, or in other words that if $r$ is a root, then so is $-1-r$. A somewhat more precise result is that $S_p(-1-x) = S_p(x)$ when $p$ is odd, and $S_p(-1-x) = -S_p(x)$ when $p$ is even (thus confirming that the polynomial $T(x) := S_p(x-1/2)$ is an odd function (has only odd powers of $x$) if $p$ is even, and is an even function (has only even powers of $x$) if $p$ is odd).

The key principle is that a polynomial is the zero polynomial iff it has infinitely many roots. For example, $f(x) = g(x)$ if $f(n) = g(n)$ for all $n \in \mathbb{N}$, and a polynomial $h$ is constant if $h(n) = h(0)$ for all $n \in \mathbb{N}$. If $h$ is a polynomial such that its first difference $(\Delta h)(x) := h(x) - h(x-1)$ satisfies $(\Delta h)(n) = 0$ for all $n \in \mathbb{N}$, then $h$ is constant with constant value $h(0)$.

Thus we have $(\Delta S_p)(x) = S_p(x) - S_p(x-1) = x^p$ and so $S_p(-x) - S_p(-1-x) = (-1)^p x^p$. For fixed $p$, put $g(x) := S_p(-1-x)$, so that $g(x-1) = S_p(-1-(x-1)) = S_p(-x)$. Thus

$$\Delta g(x) = g(x) - g(x-1) = S_p(-1-x) - S_p(-x) = (-1)^{p+1} x^p$$

which equals $\Delta S_p(x)$ if $p$ is odd, and $-\Delta S_p(x)$ if $p$ is even. Thus in the case where $p$ is odd, $\Delta(g-S_p) = 0$; applying the principle above, $g$ and $S_p$ differ by a constant: $S_p(-1-x) = S_p(x) + c$ for some constant $c$. For $x=0$, we note that $S_p(0) = 0$, and $S_p(0) - S_p(-1) = 0^p = 0$ so $S_p(-1) = 0$. It follows that $c = 0$, and we conclude $S_p(-1-x) = S_p(x)$ if $p$ is odd.

The case where $p$ is even is wholly similar. There we derive $\Delta(g + S_p) = 0$, so $g(x) + S_p(x) = c$ for some constant $c$, and we argue as before that $c = 0$, and so in this case $S_p(-1-x) = -S_p(x)$.

Answer 3

In addition to Antonio's comment/answer: Looking at the real roots (symmetrized by adding +1/2 (!)) of the 1,5,9,13,... polynomial we get the following list, where only the first three real roots are rational numbers. The rate of convergence to the half-integers is impressive... $$\small \begin{matrix} 0 & 1/2 & . & . & . & . & . & . \\ 0 & 1/2 & -1/2 & 0.763762615826 & -0.763762615826 & . & . & . \\ 0 & 1/2 & -1/2 & 0.949106003964 & -0.949106003964 & . & . & . \\ 0 & 1/2 & -1/2 & 0.999056597832 & -0.999056597832 & . & . & . \\ 0 & 1/2 & -1/2 & 0.999997848581 & -0.999997848581 & . & . & . \\ 0 & 1/2 & -1/2 & 0.999999998198 & -0.999999998198 & -1.50196566814 & 1.50196566814 & 1.74815179290 \\ 0 & 1/2 & -1/2 & 0.999999999999 & -0.999999999999 & -1.50001155318 & 1.50001155318 & 1.93305092402 \\ 0 & 1/2 & -1/2 & 1.00000000000 & -1.00000000000 & -1.50000003663 & 1.50000003663 & 1.99704558735 \\ 0 & 1/2 & -1/2 & 1.00000000000 & -1.00000000000 & -1.50000000007 & 1.50000000007 & 1.99997147602 \\ 0 & 1/2 & -1/2 & 1.00000000000 & -1.00000000000 & -1.50000000000 & 1.50000000000 & 1.99999984071 \\ 0 & 1/2 & -1/2 & 1.00000000000 & -1.00000000000 & -1.50000000000 & 1.50000000000 & 1.99999999943 \\ 0 & 1/2 & -1/2 & 1.00000000000 & -1.00000000000 & -1.50000000000 & 1.50000000000 & 2.00000000000 \\ 0 & 1/2 & -1/2 & 1.00000000000 & -1.00000000000 & -1.50000000000 & 1.50000000000 & 2.00000000000 \\ 0 & 1/2 & -1/2 & 1.00000000000 & -1.00000000000 & -1.50000000000 & 1.50000000000 & 2.00000000000 \\ 0 & 1/2 & -1/2 & 1.00000000000 & -1.00000000000 & -1.50000000000 & 1.50000000000 & 2.00000000000 \\ 0 & 1/2 & -1/2 & 1.00000000000 & -1.00000000000 & -1.50000000000 & 1.50000000000 & 2.00000000000 \end{matrix} $$ The complex roots may be fit into that pattern perhaps by their absolute values, but this naive idea is not yet convincing to me

Answer 4

Another fascinating property of the zeros of the power sums is that for all $k\geq 3$, rational part of any nontrivial zero of $S_k(x)$ is always equal to $-1/2$. This is an analogue of the Riemann Hypothesis for the power sums! See also the paper by J. Singh (2009): http://www.worldscientific.com/doi/abs/10.1142/S179304210900189X