Update
The polynomials are generated as follows:
Where
$B_n(x) = \sum_{k=0}^n {n \choose k} b_{n-k} x^k$
is used to generate standard Bernoulli polynomials, top plot is generated as follows:
$B_n^{(1)}(x) = -\sum_{k=0}^n {n \choose k} |\Re(b^{(1)}_{n-k})+ \Im(b^{(1)}_{n-k})| x^k$
using definition of $b^{(1)}_{n}$ as outlined below.
(Note: Where $b^{(1)}_{1}={\tilde{\infty}}$, substitute for usual $-\frac{1}{2}$.)
The second plot is exactly the same as above except that the first term of $B_n^{(1)}(x)$ has a positive value.
Original question
Since
$\zeta(2n) = (-1)^{n+1} \, \frac{2^{2n-1} \, b_{2n} \, \pi^{2n}}{(2n)!},\quad n \ge 0, \,$
where $b_{2n}$ are the Bernoulli numbers, rearranging & substituting $2n$ for $n$, we get:
$b_{n}^{(1)} = \frac{\zeta(n)\, n!}{(-1)^{\frac{n}{2}+1} \, 2^{n-1} \, \pi^{n}}$
Using $b_{n}^{(1)}$ to generate a series similar to the usual Bernoulli polynomials (the main difference being that the odd real $b_{n}$ are give complex values rather than 0), the roots of $B_{n}^{(1)}(x)$ differ from the usual pattern of the $B_{n}(x)$ roots and fit a scaled Szegő Curve even more tightly (bar a couple of spare roots off the diagram) than the roots of the partial sums of $e^x$ (white, outlined points):

Another curious modfication, with roots plotted against scaled Szegő Curve, circle (radius $\frac{n}{e}$) & roots of $e^x - 1$ (white, outlined points):
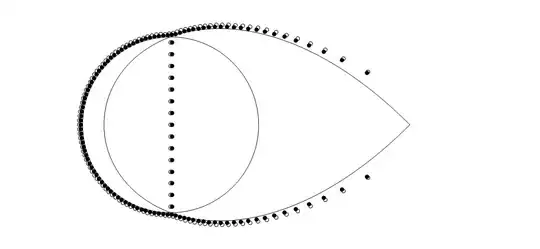
Image of the two root plots against a dynamic Szegő Curve, as given by Antonio Vargas' code below (included for comparison purposes).

Despite fairly extensive searches on the internet, I have found no literature on the subject. I was wondering if anyone knew of any?
$$B_n^{(1)}(x) = -\sum_{k=0}^n {n \choose k} |\Re(b^{(1)}{n-k})+ \Im(b^{(1)}{n-k})| x^k$$
$$where$$
$$b_{n}^{(1)} = \frac{\zeta(n), n!}{(-1)^{\frac{n}{2}+1} , 2^{n-1} , \pi^{n}},$$
$$and$$
$$b^{(1)}_{1}=-\frac{1}{2}$$
– martin Nov 07 '13 at 03:23