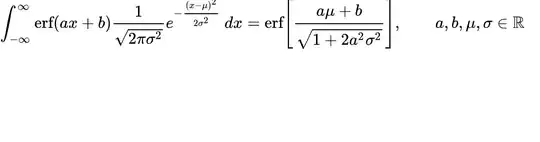I tried to evaluate the integral below using differentiation under the integral sign and error function tables [1,2,3]:
$$I = \int_{0}^{\infty} \mathrm{erfc}(ax)\exp(bx^2+cx)dx.$$
Also, the approach in this question could not be applied since, like in my case, the lower limit is $0$ instead of $-\infty$.
The application is computational modeling.
Any help will be greatly appreciated.
Since $\int \exp(b x^2+c x) dx= \frac{\sqrt{\pi } e^{-\frac{c^2}{4 b}} \text{erfi}\left(\frac{2 b x+c}{2 \sqrt{b}}\right)}{2 \sqrt{b}}$ we integrate by parts and we have: \begin{eqnarray} I&=& -\frac{\sqrt{\pi } e^{-\frac{c^2}{4 b}} \text{erfi}\left(\frac{c}{2 \sqrt{b}}\right)}{2 \sqrt{b}}- \frac{2 a}{\sqrt{\pi}} \int\limits_0^\infty \frac{\sqrt{\pi } e^{-\frac{c^2}{4 b}} \text{erfi}\left(\frac{2 b x+c}{2 \sqrt{b}}\right)}{2 \sqrt{b}} \exp(-a^2 x^2) dx\\ &=& -\frac{\sqrt{\pi } e^{-\frac{c^2}{4 b}} \text{erfi}\left(\frac{c}{2 \sqrt{b}}\right)}{2 \sqrt{b}}+\frac{e^{-\frac{c^2}{4 b}}\sqrt{\pi}}{\imath \sqrt{b}}2 T(\epsilon, \imath \frac{\sqrt{b}}{a}, \imath \frac{c \sqrt{2}}{2 \sqrt{b}} ) \\ &=& -\frac{\sqrt{\pi } e^{-\frac{c^2}{4 b}} \left(4 i T\left(\frac{i c}{\sqrt{2} \sqrt{b} \sqrt{1-\frac{b}{a^2}}},\frac{i \sqrt{b}}{a}\right)-\text{erfi}\left(\frac{c}{2 \sqrt{b} \sqrt{1-\frac{b}{a^2}}}\right)+\text{erfi}\left(\frac{c}{2 \sqrt{b}}\right)\right)}{2 \sqrt{b}} \end{eqnarray} where in the second line we took a small number $0 < \epsilon << 1$ and we used the definition of the generalized Owen's T function Generalized Owen's T function and in the last line we simplified the result. Here $T(\cdot,\cdot)$ is the Owen's T function. The result is valid for $0 < b < a^2$.
In[697]:= {a, c} = RandomReal[{0, 3}, 2, WorkingPrecision -> 50];
b = RandomReal[{0, a^2}, WorkingPrecision -> 50]; eps = 10^(-9);
NIntegrate[Erfc[a x] Exp[b x^2 + c x], {x, 0, Infinity}]
-((E^(-(c^2/(4 b))) Sqrt[\[Pi]] Erfi[c/(2 Sqrt[b])])/(2 Sqrt[b])) +
2/Sqrt[Pi] a NIntegrate[(
E^(-(c^2/(4 b))) Sqrt[\[Pi]] Erfi[(c + 2 b x)/(2 Sqrt[b])])/(
2 Sqrt[b]) Exp[-a^2 x^2], {x, 0, Infinity}]
-((E^(-(c^2/(4 b))) Sqrt[\[Pi]] Erfi[c/(2 Sqrt[b])])/(2 Sqrt[b])) + (
E^(-(c^2/(4 b))) Sqrt[ Pi])/(I Sqrt[b])
NIntegrate[
Erf[I (c + 2 b /(Sqrt[2] a) x)/(2 Sqrt[b])] Exp[-1/2 x^2]/Sqrt[
2 Pi], {x, 0, Infinity}]
-((E^(-(c^2/(4 b))) Sqrt[\[Pi]] Erfi[c/(2 Sqrt[b])])/(2 Sqrt[b])) + (
E^(-(c^2/(4 b))) Sqrt[ Pi])/(I Sqrt[b])
2 T[eps, I b /(a Sqrt[b]), I (c Sqrt[2])/(2 Sqrt[b])]
-((E^(-(c^2/(4 b)))
Sqrt[\[Pi]] (Erfi[c/(2 Sqrt[b])] -
Erfi[c/(2 Sqrt[b] Sqrt[1 - b/a^2])] +
4 I OwenT[(I c)/(Sqrt[2] Sqrt[b] Sqrt[1 - b/a^2]), (I Sqrt[b])/
a]))/(2 Sqrt[b]))
Out[699]= 0.789518
Out[700]= 0.789518
Out[701]= 0.789518 + 0. I
Out[702]= 0.789518482586510679235860756093903252836337770103 +
0.*10^-59 I
Out[703]= 0.789518482636559413924687222227564264392988055015
Here in this question you can refer to this integral.
Well this might prove useful might not be good solution just noticed it.
