0

After my last SE question on confidence Intervals here, which clarified the intuition, I tried then to verify statistical results if they are convincingly compliant with theory. I started with CI for Sample Proportions and tried some combinations as below.

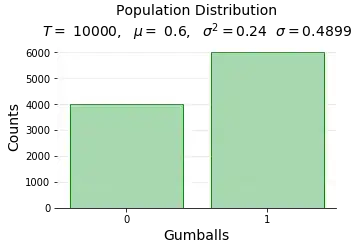
Step 1: Created Population I created a 10000 sized population with sample proportion of 60% for success. For eg, 10000 balls with 60% yellow balls. Below is my distribution graph.

enter image description here

Step 2: Sampling distribution (fixed sample size, fixed no of experiments) I then sampled from population, for N times (no of experiments), each time for sample size of n. Below is my sampling distribution (with sample mean and SD).
enter image description here

Step 3: Confidence Interval (fixed sample size, fixed no of experiments) Since population SD is known, I calculated CI as below for 95% confidence interval. N was 100, n was 50.
$$ \color{blue}{CI = Y + 1.96 \dfrac{\sigma}{\sqrt{n}}} \tag{1} $$ I got the results plotted as below. 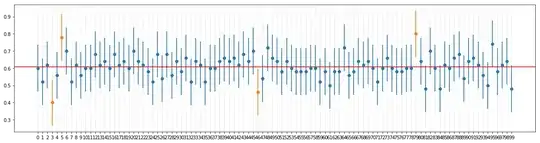enter image description here So far so good.

Step 4: Varying Experiment Size, Varying Sample Size I wanted to check results for different combinations. Currently we applied Z transform because, $np = 50(0.6) = 30 \geq 10$. Also population SD because we know that. What if we do not know that? Can we apply sample SD? And what if I apply biased sample SD? And what happens when I apply t transformation (df included)? I wanted to see a convincing visualization statistically, so as to say, why for sample proportions we choose to use Z transform, and population mean. If pop.mean not known, why any other combi could be better? (for eg, Z with unbiased sample SD combo?)

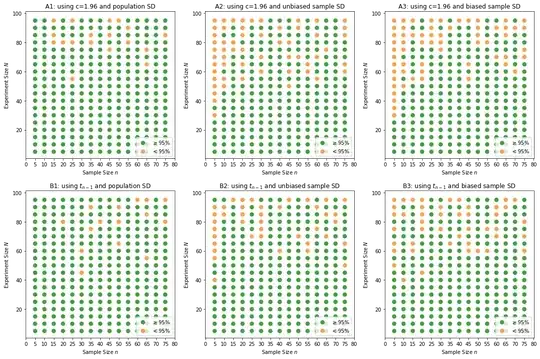
Below is result of me varying sample size and also experiment sizes. Any dot (green or red), indicates for that sample size, conducted over those many no of times (experiment size), if green means it yielded a set of CIs, in which, 95% or more contain population mean, red otherwise.

enter image description here

Inferences and questions - Part 1: 1. Chart A1 looks definitely better, so is chart B1 too. So can we apply t as well, with population mean?
2. For both Z and t, there is no much difference between biased or unbiased sample SDs. Check not much difference between A2 and A3, and so are B2 and B3. Does this mean, we could use biased SD also with not much difference in results? 3. Or these images do not feel just right and problem could be in my code? My code is added in link below.

Step 5: Higher no of experiments till 500.

Earlier test was not very consistent except above points. So when I upped my no of experiments till 500, to see if any consistency could be spotted, I was shocked to see, the accuracy or performance simply reduced drastically. Very very poor show here.
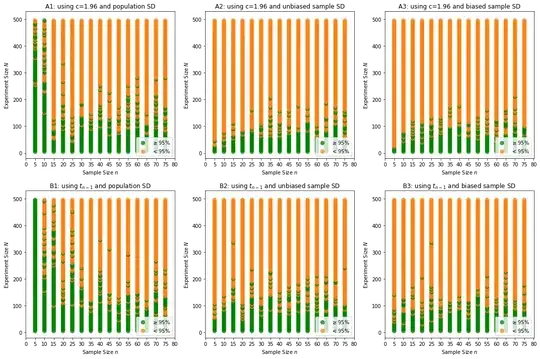
enter image description here

Inferences and questions - Part 2: 4. Why did this happen? Is it something expected? I thought with more and more sample means, only my distribution becomes better normal, so CIs should perform better. But it only has gone worse. What could be issue theoretically? Or could my program be issue and this is never meant to happen? Theoretically outcomes are surely wrong? (if programming issue, I could port this question accordingly)

References: 1. My entire code for above images is here 2. Dependent files are here. SDSPSM.py, ci_helpers.py

Update 25th Aug 2018: Finally solved. It was a silly bug in the program during calculating accuracy. Should divide by each_N instead of 100. Thank you Adam

Parthiban Rajendran
  • 445

1 Answers1

0

Treatment of this example has a couple of problems:

(1) This was intended as an example for a problem of forming an approximate confidence interval for a Normal distribution with unknown mean and standard deviation (two unknown parameters). This example uses the Binomial distribution which has only one unknown parameter (the probability of success, $p=0.6$) since the sample size is known.

(2) Since the Binomial is a discrete distribution, the construction for the confidence belt is complicated. For every value of $p$ there is approach to select exactly 95% of outcomes, so a set of outcomes is chosen with at least 95% of outcomes. Some papers explain different approaches,

for example: https://www.jstage.jst.go.jp/article/jjss1970/23/2/23_2_161/_pdf/-char/ja

I recommend that you sample from a normal distribution to investigate the properties of your approximate confidence interval (and the exact approach using the confidence belt formed using the Student's t distribution).

Dean
  • 1,370
  • yeah, but population parameters are just there to verify our outcomes, though in real life it may not be the case. I hesitate to have population distribution also as normal, because then sampling distributions is guaranteed to be normal for any n or p, so the little nuances (limiting conditions) do not show up. I wanted to take just a random sample and still prove 95% CIs work as expected. Bernoulli for sample proportions and random next for sample means (once above doubts clarified). I will check paper, but any more insights on why this poor performance could occur? – Parthiban Rajendran Aug 20 '18 at 18:53
  • First of all, I see no reason why you complicate your figures and explanation with showing results with different N. To validate a method to produce confidence intervals you should use a very large number of repetitions (N) and confirm that the correct fraction of the confidence intervals contain the true parameter. It is not interesting to see if 95% of 5 repetitions contain the true parameter! Fix N to be large (like 10,000) and show the fraction of intervals containing the true parameter as a function of sample size. – Dean Aug 21 '18 at 00:10
  • Second of all, because you chose the binomial distribution for which the standard deviation and the expectation are related, you may have a situation like example 4 of the original explanation... in which case, the approximation you are applying is a poor one. – Dean Aug 21 '18 at 00:13
  • Finally, my recommendation for you to start with a normal distribution, was that you could see that for small sample sizes the approximate method you use is not valid, whereas for large samples (or by using the correct treatment of small samples using the t-distribution critical values) you get valid confidence intervals. – Dean Aug 21 '18 at 00:15
  • But @Dean, just for N=500, I am getting poor performance, and it goes poorer with increasing N, so how would it be better in N=10000, (actually total population size =10000)? And which is example 4 you are referring to? – Parthiban Rajendran Aug 21 '18 at 06:34
  • For random/bernoulli, the minimal condition to apply normal approximation is $np \geq 10$ but some say even $np \geq 5$ or even 15 so I started at 5. Further my focus is mainly on larger N, why performance becomes poorer. Where exactly my approximation becomes invalid at large N values? In fact, with $n=50$, and $p=0.6$, we already cross $np = 30$ threshold so anything beyond that should give us better results? But that was not happening in mine.Why poor performance of my approximation, when I am way beyond $np$ threshold – Parthiban Rajendran Aug 21 '18 at 06:35
  • And N=500 is just 5% of T. After 10% of T, unless replaced, the samples would no more be independent as a general rule. So I have not even broken that also, to get a poor performance. I also tried with sampling with replacement, but got same results. – Parthiban Rajendran Aug 21 '18 at 06:44