1

This is a follow up question after solving related problem here

I started with CI for Sample Proportions and tried some combinations as below.

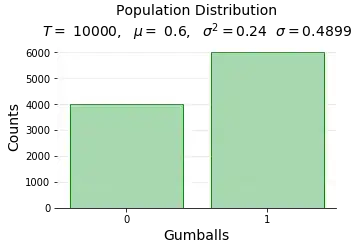
Step 1: Created Population I created a 10000 sized population with sample proportion of 60% for success. For eg, 10000 balls with 60% yellow balls. Below is my distribution graph.

enter image description here

Step 2: Sampling distribution (fixed sample size, fixed no of experiments) I then sampled from population, for N times (no of experiments), each time for sample size of n. Below is my sampling distribution (with sample mean and SD).
enter image description here

Step 3: Confidence Interval (fixed sample size, fixed no of experiments) Since population SD is known, I calculated CI as below for 95% confidence interval. N was 100, n was 50.
$$ \color{blue}{CI = Y + 1.96 \dfrac{\sigma}{\sqrt{n}}} \tag{1} $$ I got the results plotted as below. 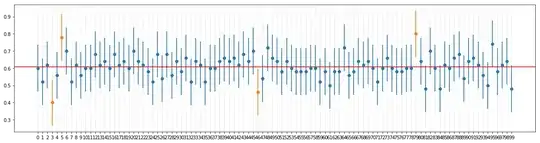enter image description here So far so good.

Step 4: Varying Experiment Size, Varying Sample Size I wanted to check results for different combinations. Currently we applied Z transform because, $np = 50(0.6) = 30 \geq 10$. Also population SD because we know that. What if we do not know that? Can we apply sample SD? And what if I apply biased sample SD? And what happens when I apply t transformation (df included)? I wanted to see a convincing visualization statistically, so as to say, why for sample proportions we choose to use Z transform, and population mean. If pop.mean not known, why any other combi could be better? (for eg, Z with unbiased sample SD combo?)

Below is result of me varying sample size and also experiment sizes. Any dot (green or red), indicates for that sample size, conducted over those many no of times (experiment size), if green means it yielded a set of CIs, in which, 95% or more contain population mean, red otherwise.

I got below result:
enter image description here

Questions:

From the output, I get below inferences.

  1. If population SD is known, no matter Z or T distribution used, it is 100% surety that, the CIs of sample sets of any distribution of sample size and experiment size, will contain population mean 95% of the time.(indicated by totally green graphs on left on both rows). Is this inference correct?
  2. There is not much a difference between using unbiased or biased sample SD irrespective of Z or T distribution. So why favor unbiased sample SD?
Parthiban Rajendran
  • 445

1 Answers1

0
  1. This isn't strictly correct except when the population is normally distributed, which it isn't here. Even when the population is normally distributed, it can still happen that your collection of confidence intervals in particular contains the population mean a somewhat different fraction of the time. In any case, this statement is "morally correct", the issues are just with technicalities.
  2. For large $n$ the two are close together, of course. An advantage of the unbiased one is that it's well studied, so for instance it is for the unbiased sample standard deviation that we know that $\frac{\sum_{i=1}^n X_i - n \mu}{S\sqrt{n}}$ is $t$-distributed. It isn't quite $t$-distributed in the biased version.

As a followup remark, in practice neither the population mean nor the population standard deviation is ever known, so the $t$ distribution version is, in practice, always what you want to do when estimating the population mean (assuming the underlying distribution and sampling method satisfy CLT of course).

Ian
  • 101,645
  • thank you @Ian. I ran above setup couple of times, and every time for point (1) I got 100% (that is, 95% of CIs always contained population mean). And that this worked for a bernoulli population distribution. So wondering theoretically is this a surety some how that could be derived? For point (2) as you can see in results, I do not see much difference between unbiased and biased, and obviously lowering $n$ would affect performance anyway, so is there any other way to show superiority of unbiased SD in my approach? – Parthiban Rajendran Aug 27 '18 at 05:47