8

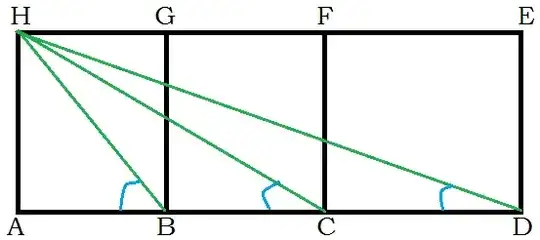
We know about the famous 3-square problem.

Draw three adjacent squares with same size and any two adjacent square has a common side. This looks like a rectangle. Name all of the vertices of square in anti clock wise from $A$ to $H$. Join $HB$, $HC$, and $HD$. Prove that $$\angle{ABH}+\angle{ACH}+\angle{ADH}=90^\circ$$

enter image description here

Visual proof of 3-square problem. In this figure we can find three congruence right-angled triangles which are in yellowish-green color and their hands are in ratio $2:1$ and we can see two isosceles right angled triangle. Orange colored angle symbol denote half right angle (i.e,$45^\circ$).

enter image description here

In square $ABGH$, $HB$ is the diagonal of square. By using the property of diagonal of square we get, $\angle{ABH}=45^\circ$. We also know that $\angle{ABH}+\angle{ACH}+\angle{ADH}=90^\circ$.

From above two equations, we get $\angle{ACH}+\angle{ADH}=45^\circ$. $\square$

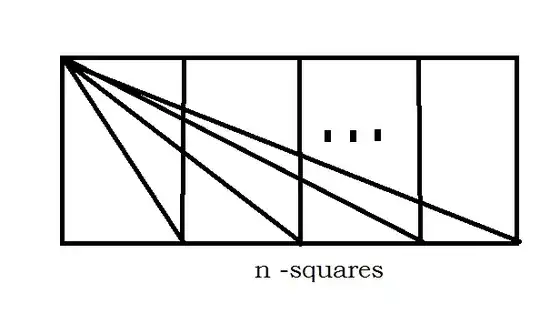
Now, for my question:

Let $n$ be the number of squares. Is it possible, for $n$-squares, for the sum of all angles which lies below each line to became $180^\circ$?

enter image description here

Blue
  • 75,673
  • 3
    very nice visual proof. – NEW SUN May 29 '18 at 13:45
  • Numerical calculation indicates that if we continue the series with consecutive terms having the form $\arctan(1/n)$ the sum misses 180°. – Oscar Lanzi May 29 '18 at 13:57
  • 2
    This is easy enough to check with a calculator. For $n=16$, the angle sum is $177.947\ldots^\circ$; for $n=17$, the sum is $181.313\ldots^\circ$. – Blue May 29 '18 at 13:59
  • Related questions: More proofs of the 3-square puzzle are here. (My own is here.) Differences in the sums for $10^x$ squares are here. Taking the limit as the number of squares increases without bound, here. – Blue May 29 '18 at 14:15

1 Answers1

6

The question being asked is whether or not

$$S_n=\sum_{k=1}^n\arctan\left(1\over k\right)$$

is ever equal to $\pi$ (expressed in radians, or $180$, in degrees). By calculation one finds

$$S_{16}\approx3.1057646\lt\pi\lt3.16452042\approx S_{17}$$

so the answer is No. It'd be nice, though, to have a less computationally-dependent answer (along the lines of the proof that $\sum_{k=1}^n{1\over k}$ is never an integer for $n\gt1$).

Remark (added later): The identity

$$\arctan\left(1\over x\right)={\pi\over2}-\arctan x\quad\text{if }x\gt0$$

means you can relate this to a 2007 paper by Tewodros Amdeberhan, Luis A. Medina, and Victor H. Moll, in which they study the sequence

$$x_n=\tan\left(\sum_{k=1}^n\arctan k \right)$$

which, by virtue of the addition formula for the tangent function, satisfies the recursion equation

$$x_n={x_{n-1}+n\over1-nx_{n-1}}\quad\text{with }x_1=1$$

This gives the sequence

$$1,-3,0,4,-{9\over19},{105\over73},-{308\over331},{36\over43}\cdots,$$

The OEIS extends the sequences of numerators and denominators.

Amdeberhan et al. prove that $1-nx_{n-1}\not=0$ for $n\gt1$, so that the $x_n$'s are all well-defined rational numbers, and that $x_n\not=0$ for $n\ge4$. Together these imply that the OP's sum, $S_n$, is an integer multiple of $\pi\over2$ only for $n=3$, which is a way of ruling out $S_n=\pi$ without an explicit computation of $S_{16}$ and $S_{17}$. The proof, however, is not at all geometric.

Barry Cipra
  • 79,832