Is it possible to explain geometrically why $\arctan (1/2) +\arctan (1/3) = 45$ degrees?

Question

$\arctan(1/2)$ seems to be some strange, irrational angle, and the same goes for $\arctan(1/3)$, but those two angles seem to sum up to $45$ degrees. This seems like a mystery to me even though I can derive the result algebraically as follows, by using the summation formula for the tangent function.

$\tan\big(\arctan(1/2)+\arctan (1/3)\big)=\dfrac{5/6}{1 - 1/6}=1\,.$

Can someone come up with a geometric explanation?

A remark: I started thinking about the described arctan puzzle while I was trying to solve a problem in complex analysis, namely this one:

How to find a conformal mapping which maps the region between |z + 3| < √ 10 and |z − 2| < √ 5 onto the interior of the first quadrant?

Answer 1

There are many good geometric renderings; my favorite invokes the familiar Red Cross symbol. This symbol consists of a central square block sharing each of its edges with an additional congruent block. We superpose right triangle $ABC$ and label some additional vertices $D,E,F$ as shown below.

$\triangle \space ACD$ and $CBE$ are right triangles with congruent legs, so congruent triangles by SAS; thus their hypotenuses which are also legs of right $\triangle ABC$ are congruent. So the acute angle $BAC$ measures $45°$. But the component of that angle within right $\triangle ACD$ measures $\arctan(1/2)$ and the remaining component within right $\triangle ABF$ measures $\arctan(1/3)$. Thereby $\arctan(1/2)+\arctan(1/3)=45°$.

Answer 2

Let us take $\triangle ABC$ with $AB=3, BC=4, CA=5, \angle B = 90^\circ$. Let the angle bisectors $AI, BI, CI$ meet at incenter $I$. From $I$ drop perpendiculars $ID,IE,IF$ onto the sides. The inradius is $ID=IE=IF=1$. Clearly $BFID$ is a square, so $BF=BD=1$, $AF=AE=2$, $CD=CE=3$. This leads to the angles as in the following diagram.

Thus $\frac{A}{2}=\tan^{-1} \frac{1}{2}$, $\frac{C}{2}=\tan^{-1} \frac{1}{3}$. But $A+C=\frac{\pi}{2}$ means $$\frac{A}{2}+\frac{C}{2}=\tan^{-1} \frac{1}{2}+\tan^{-1} \frac{1}{3}=\frac{\pi}{4}$$ As a bonus, adding the six angles formed at the incenter gives $$2\tan^{-1} 1 + 2\tan^{-1} 2 +2\tan^{-1} 3 =2\pi$$ $$\Rightarrow \tan^{-1} 1 + \tan^{-1} 2 +\tan^{-1} 3 =\pi$$

Similar dissections of other right triangles $\{(5,12,13),$ $(7,24,25), \ldots\}$ will give new identities involving $\tan^{-1} (\text{rational number})$.

Answer 3

Just a comment on the beautiful answer of @Oscar Lanzi:, if we add four strips of width $1$ and length $x$ to a square of side $1$, we get again a cross with an inscribed square, and the equality

$$\arctan \frac{1}{2x + 1} + \arctan\frac{x}{x+1} = \frac{\pi}{4}$$

$\bf{Added:}$ In the picture below, the yellow segments have length $1$, the light blue have length $x$.

$\bf{Added:}$ With the same method, with some care, we can prove the addition formula for the tangent. Indeed, consider two rectangles with sides, $a$, $b$ , and two with sides $t a$, $t b$. (in the picture below, sides $2,5$ and $4$, $10 $) . Arrange them so we from their diagonals we get a rectangle with the ratio of the sides $t$. Then we get the formula

$$\arctan \frac{a}{b} + \arctan\frac{t b - a}{t a + b} = \arctan t$$

In our case

$$\arctan\frac{2}{5} + \arctan\frac{8}{9} = \arctan 2$$

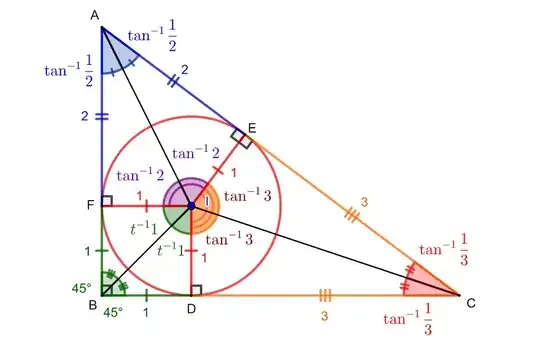
Note: If we start from an arbitrary symmetric cross we might not get a rectangle, but only a parallelogram, so we modified the approach a bit. In general, to get a cross that produces a rotated rectangle, start with a container rectangle and intersect its sides with a central circle.

Answer 4

With $0 < a < b,$

$$ \arctan \frac{a}{b} + \arctan \frac{-a+b}{a+b} = \frac{\pi}{4} $$

as vectors, in order to add the angles, we need to ask the angle between vectors $v=(-1,2)$ and $w=(1,3).$ This is what I was doing in answering your previous question.

$$ \cos \theta = \frac{v \cdot w}{|v| \; |w|} = \frac{5}{ \sqrt 5 \; \sqrt{10}} = \frac{5}{\sqrt{50}} $$

so $$ \cos \theta = \frac{5}{5 \sqrt 2} = \frac{1}{ \sqrt 2} $$

We get something similar with $v=(-1,5)$ and $w=(2,3).$

Or with $v=(2,5)$ and $w=(-3,7).$

Or with any integers $0 < a < b,$ vectors $v=(a,b)$ and $w=(a-b,a+b).$

Answer 5

Just to add to the variety of many fine geometrical answers, express the measures of the following three angles in terms of arctangent and compare the results:

$$ \angle CAD, \angle DAB, \angle CAB $$