5

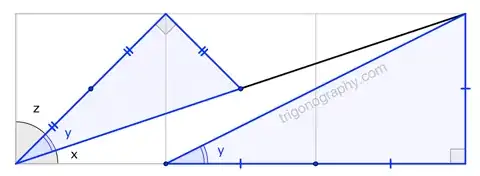
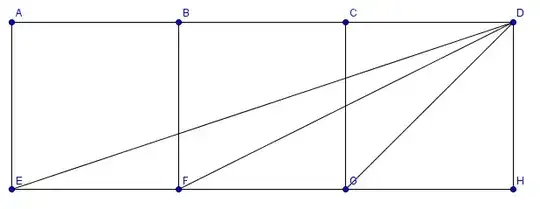
How can I show that $x+y=z$ in the figure without using trigonometry? I have tried to solve it with analytic geometry, but it doesn't work out for me. 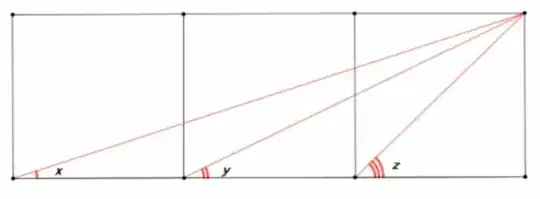enter image description here

Mohsen Shahriari
  • 6,718
Hamid Mohammad
  • 161
  • 1
  • 1
  • 7

5 Answers5

6

enter image description here

(This space intentionally left blank.)

Blue
  • 75,673
3

Hint: denoting the points like on the picture below, triangles $EGD$ and $DGF$ are similar (why?).

enter image description here

Wojowu
  • 26,600
2

Let $X$, $Y$, and $Z$ be the apexes of the angles $x$, $y$, and $z$, respectively. Also, let $P$ be the common intersection of the red lines. Show that $ZP^2=ZX\cdot ZY$. Thus, the circumcircle of the triangle $PXY$ is tangent to $PZ$ at $P$. This will prove that $\angle YPZ=\angle YXP=x$.

Batominovski
  • 49,629
0

Equivalently, you have to prove that $$ \underbrace{\mathrm{arctan}(1/3)}_{x}+\underbrace{\mathrm{arctan}(1/2)}_{y}=\underbrace{\mathrm{arctan}(1)}_{z}. $$ This is pretty clear by addition of tangents, indeed $$ \tan(x+y)=\frac{\tan(x)+\tan(y)}{1-\tan(x)\tan(y)}=1 \implies x+y=\frac{\pi}{4}. $$

Paolo Leonetti
  • 15,423
  • 3
  • 24
  • 57
-1

Imagine that all the the squares are 1 by 1 and so the rectangle has base 3 and a height of $1$.

There are three right-angled triangles in the diagram. The one with angle $x$ has base 3, and height 1. The triangle with angle $y$ has base 2 and height 1. The triangle with angle $z$ has base 1 and height 1.

Using the standard trig' ratio $\tan \theta = \frac{\mathrm{opp}}{\mathrm{adj}}$, we get $\tan x = \frac{1}{3}$, $\tan y = \frac{1}{2}$ and $\tan z= \frac{1}{1}=1$.

There is a well-know formula for angle addition:

$$\tan(\alpha+\beta) = \frac{\tan \alpha + \tan \beta}{1-\tan \alpha \tan \beta}$$

Applying this formula to the case of $\alpha =x$ and $\beta = y$ gives: $$\tan(x+y) = \frac{\tan x + \tan y}{1-\tan x \tan y}=\frac{\frac{1}{3}+\frac{1}{2}}{1-\frac{1}{3}\cdot\frac{1}{2}}=1$$ It follows that $\tan(x+y)=\tan z$. Since $0^{\circ} < x<y<z < 90^{\circ}$ it follows that $$\tan(x+y) = \tan z \iff x+y = z$$

Fly by Night
  • 32,272
  • "... without using trigonometry?" – Blue Jan 09 '16 at 22:36
  • @Blue All of the answers given so far involve trigonometry to some degree, even yours. The fact that you don't mention sine, cosine or tangent is irrelevant. The answer to the OP's question should be: no such answer exists. Trigonometry is the science of triangles using lengths, angles and their ratios. I could re-phrase my answer in terms of lengths and proprtion, but that's really just trigonometry, but without the nice simple place-holders of sine, cosine and tangent. – Fly by Night Jan 09 '16 at 22:40
  • If you use trigonometry for a question that asked for an answer without trig, than you are obligated to define all your terms and identitities. – fleablood Jan 09 '16 at 22:51
  • And you certainly can not simply say "there is a well known identity" unless you actually prove it. – fleablood Jan 09 '16 at 22:52
  • 1
    @fleablood You're absolutely right. I hadn't read the "without trigonometry" until after I'd written my answer. However, being asked to solve this problem without trigonometry is, like I said, being asked to solve it without using angles, lengths, and their ratios. I'll leave my answer here because I think it might help people who Google this question in the future, and who are willing to use trigonometry to solve problems involving triangles. – Fly by Night Jan 09 '16 at 22:55
  • Technically speaking, everything we learn of similar triangles in geometry is a form of trig. But the student who hasn't study trig doesn't know what trig is. Blue's answer is accessible to a geometry student. Yours is not. – fleablood Jan 09 '16 at 23:09
  • @FlybyNight: As a self-styled "trigonographer", I certainly agree that trigonometry is the study of triangle measurements. (It's in the name!) So, sure, if we're being pedantic, a trig-less solution to an angle-sum problem is an impossibility. (In fact, I considered adding a disclaimer to this effect on my answer. :) That said, we reasonably read "without using trigonometry" as OP's hope to avoid sophisticated trigonometric machinery. My sol'n involves trig (as it must), but only at its most-fundamental level: identifying and exploiting similar triangles. sin/cos/tan stuff isn't necessary. – Blue Jan 09 '16 at 23:32
  • 1
    @Blue I agree. Your solution is great! – Fly by Night Jan 09 '16 at 23:42
  • 1
    @fleablood Be careful with the accessibility statement. We teach children trigonometry from the ages of 13/14 in the UK. The angle addition formulae come along at around 16/17. My answer is perfectly accessible for someone able to generate the graphic like the OP did. It's not like I'm using cohomology. – Fly by Night Jan 09 '16 at 23:45