2

Prelude

While studying trigonometry, I came across this very interesting problem. It wasn't very difficult to solve, however it's result was quite interesting. I have given the solution below. Try to solve it yourself before looking.

Problem

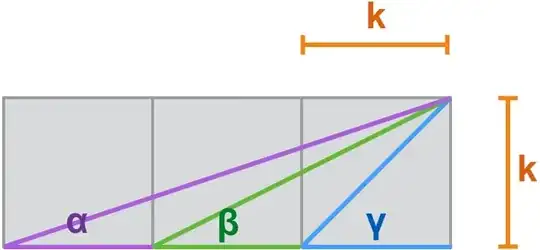
The diagram below shows three equal squares, with angels $\alpha$, $\beta$, $\gamma$ as marked. Prove that $ \alpha + \beta = \gamma $.

diagram

Hint

If you are not in the midst of a trigonometry course, chances are you will need to see this hint, as it is an uncommon identity.

Hover below to see a hint.

$ \arctan a + \arctan b = \arctan{\frac{a + b}{1 - ab}} $

This identity was solved earlier in the book I found this problem in (see Postscript). Try to prove this identity for yourself, too!

Postscript

This problem came from the textbook: "Trigonometry" by I. M. Gelfand.

Fine Man
  • 1,671
  • I know this this not the place to ask, but how do you hide your hint? I've been trying to figure that out for ages. – Hamed Jul 02 '16 at 00:30
  • 1
    @Hamed -- I just learned how to do so 2 minutes before I posted this question. :) You can find out here. – Fine Man Jul 02 '16 at 00:31
  • @Blue -- Actually, it's not really a duplicate. The OP of the question you linked asked for a non-trig solution. However, anything goes for this one. – Fine Man Jul 02 '16 at 00:41
  • @SirJony: People may have seen it mentioned by Numberphile a couple of years ago. As I note in my Trigonography entry, the puzzle was featured by Martin Gardner in 1996, and dates back to at least 1971. – Blue Jul 02 '16 at 00:46
  • @Blue -- Oh, that's interesting. I'd never heard of this problem before reading Gelfand's book. Thanks for the history and other references! However, does this still make my question a duplicate, if it hasn't been asked (trig-style) on Math SE before? – Fine Man Jul 02 '16 at 00:49

1 Answers1

1

Proof

Step 1: Gather information from diagram.

  • $ \alpha = \arctan \frac{1}{3} $
  • $ \beta = \arctan \frac{1}{2} $
  • $ \gamma = \arctan 1 $

Step 2: Add $\alpha$ and $\beta$ and simplify.

$ \alpha + \beta = \arctan \frac{1}{3} + \arctan \frac{1}{2} = $

...Now, using an identity (see hint given in the question)...

$ = \arctan {\frac{\frac{1}{3} + \frac{1}{2}}{1 - \frac{1}{3}\frac{1}{2}}} = \arctan {\frac{\frac{5}{6}}{1 - \frac{1}{6}}} = \arctan {\frac{\frac{5}{6}}{\frac{5}{6}}} = \arctan 1 = \gamma $

Answer

Indeed, $$ \alpha + \beta = \gamma $$

Fine Man
  • 1,671