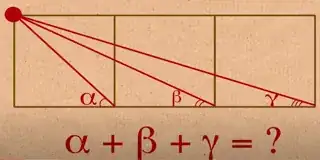So I was watching an "old" video from Numberphile, "The Three Square Geometry Problem". Here is a screenshot:
It's pretty easy to see that the sum of three angles is 90°, but now I am curious: What if we keep going on? What if we had more than 3 squares and with that more than 3 angles? What would the sum be?
Basically I want to find the value of: $$\lim\limits_{n \rightarrow \infty}\sum\limits_{k=1}^n \arctan\left(\frac{1}{\sqrt{k^2+1}}\right)$$
If there is an answer I would like to know it. Thank you.
P.S. $\arctan$ stands for $\tan^{-1}$