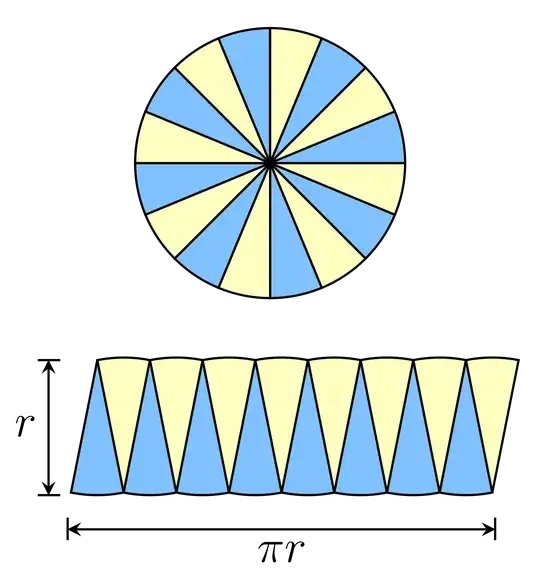
If you take on blind faith that the area of a circle with radius 1 is $\pi$, then you can calculate $\pi$ without trigonometry by taking the power series of $2\sqrt{1 - x^2}$ and integrating it from -1 to 1. The problem is any proof from first principles that the area of a circle with radius 1 is $\pi$ uses trigonometry. First I will calculate $\pi$ directly from its technical definition without using the assumption that the area of a circle with radius 1 is $\pi$. Next, I will prove from first principles that the area of a circle with radius 1 is $\pi$. I don't consider this image a proof from first principles that the area of a circle with radius 1 is $\pi$.
Here's a calculation of $\pi$ directly from the definition.
It's obvious that $\pi = 6 \times \sin^{-1}(\frac{1}{2})$. It turns out that the derivative of $\sin^{-1}$ is an elementary function. All we have to do is figure out the power series for the derivative of $\sin^{-1}$ centered at 0 and then integrate each term to get the power series for $\sin^{-1}$. In general, $\frac{d}{dx}f^{-1}(x) = \frac{1}{f'(f^{-1}(x))}$. So $\frac{d}{dx}\sin^{-1}(x) = \frac{1}{\cos(\sin^{-1}(x))} = \frac{1}{\sqrt{1 - x^2}} = (1 - x^2)^{-\frac{1}{2}}$. To take the power series of this centered at 0, you first take the power series of $(1 + x)^{-\frac{1}{2}}$ centered at 0 and then substitute $-x^2$ for $x$. Now the first derivative of this is $-\frac{1}{2}(1 + x)^{-1\frac{1}{2}}$. Then the second derivative is $(-\frac{1}{2})(-1\frac{1}{2})(1 + x)^{-2\frac{1}{2}}$. Now to get its power series, you divide the derivatives by the factorials to get $(1 + x)^{-\frac{1}{2}} = 1 - \frac{1}{2}x + \frac{1}{2}(\frac{3}{4})x^2 - \frac{1}{2}(\frac{3}{4})(\frac{5}{6})x^3 ...$ Now substituting $-x^2$ for $x$, we get $(1 - x^2)^{-\frac{1}{2}} = 1 + \frac{1}{2}x^2 + \frac{1}{2}(\frac{3}{4})x^4 + \frac{1}{2}(\frac{3}{4})(\frac{5}{6})x^6 ...$ Now finally, $\sin^{-1}(x) = \int_0^x(1 - t^2)^{-\frac{1}{2}}dt = x + \frac{1}{2}(\frac{1}{3})x^3 + \frac{1}{2}(\frac{3}{4})(\frac{1}{5})x^5 + \frac{1}{2}(\frac{3}{4})(\frac{5}{6})(\frac{1}{7})x^7$. So $\pi = 6 \times \sin^{-1}(\frac{1}{2}) = 6(2^{-1} + \frac{1}{2}(\frac{1}{3})(2^{-3}) + \frac{1}{2}(\frac{3}{4})(\frac{1}{5})(2^{-5}) + \frac{1}{2}(\frac{3}{4})(\frac{5}{6})(\frac{1}{7})(2^{-7}) ...)$.
Here's a proof that the area of a circle with radius 1 is $\pi$.
Using the substitution rule in reverse, we get $\int_{-1}^12\sqrt{1 - x^2} = 2\int_{-1}^1\sqrt{1 - x^2} = 2\int_{-1}^1\cos(\sin^{-1}(x)) = 2\int_{\sin(-\frac{\pi}{2})}^{\sin(\frac{\pi}{2})}\cos(\sin^{-1}(x)) = 2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos(\sin^{-1}(\sin(\sin'(x)))) = 2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos^2(x) = 2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{\cos(2x) + 1}{2} = \pi$
Image source: Area of a circle $\pi r^2$
