Area of a circle $\pi r^2$

Question

So, today I learned that the area of a circle is $\pi r^2$. So, I thought that since $r$ is $1$ dimensional, $r^2$ will be $2$ dimensional. In this case, a square, as you only multiply $2$ dimensions (without additional manipulation to change the shape).

But then, what does $\pi$ do to the square? How can a square become a circle with $\pi$?

Possible answers that I thought are that the area of the circle is equal to $3.1415\ldots$ squares (with $r$ side length). And that the formula $\pi r^2$ is derived from a long formula(I would like to know the long formula if this is true, because how do mathematicians get the area of the circle before comparing in the first place?)

I asked my teacher about this but he can't really understand me. So, I hope experts at StackExchange understand my problem.

A picture I drew, showing that $r^2$ is a square

Answer 1

I guess you already know that the perimeter of the circle is $2\pi$. This means that a string that covers all the perimeter of the circle will be $2\pi$ (around 6.3) times larger than a string going from the center to the boundary of the circle. This ratio is constant and only depends on the figure itself being a circle, but not on its size (the formula is valid for any radius).

Now imagine you draw very small triangles like the ones in this figure

In a sense this is like cutting pizza slices, but pizza slices are curved on the outside. However, if you make the slices very very thin, then they will be almost like triangles, and putting them together you can apply the formula for the area of a parallelogram, base times height. Therefore, $$ A = r \times \pi r = \pi r^2 $$

From this last picture you can already see that the area of a circle of radius $r$ is going to be $\pi$ times larger than the area of a square of side $r$, because in the case of the circle you can "cut it" in slices and transform it to a rectangle, with one side of size $r$ (as in the square) but with the other side $\pi$ times larger. If you wanted to make a square with the same area, you would need to "redistribute" this area excess between its sides. Specifically, its sides should satisfy the following expression $$ s^2 = \pi r^2 $$ because $s^2$ is exactly the area of the square (we called the side of the square "$s$"). Now, if two quantities are equal, so are their square roots, so taking the square root to each side of the last expression we obtain $$ c = \sqrt{\pi} \times r $$ This means that to get a square with the same area as a circle, its side needs to be $\sqrt{\pi} \simeq 1.77$ times the radius of the circle.

Answer 2

You are correct that the $r^2$ term in some sense makes the area. What the formula $A = \pi r^2$ says is that the area of the circle is larger than the area of the square with side $r$ (as you can clearly see by your drawing).

More precisely, the area of the circle is the same as the area of the square with side $\sqrt{\pi}\cdot r$ because $(\sqrt{\pi}\cdot r)^2 = \pi r^2$. So what you can say is that the $\pi$ scales the length of the sides properly.

Answer 3

In physical units, $r$ is a number with an associated unit of distance, say a meter ($m$). $r^2$ is a number with an associated unit of area, $m^2$. But $r^2$ is not a square, it is the area of a square. Squaring is an arithmetical operation, not a geometrical one. It maps numbers to numbers, not shapes to shapes.

Answer 4

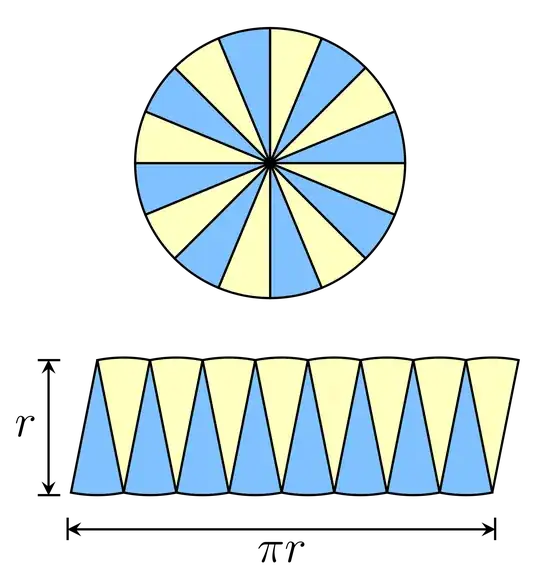
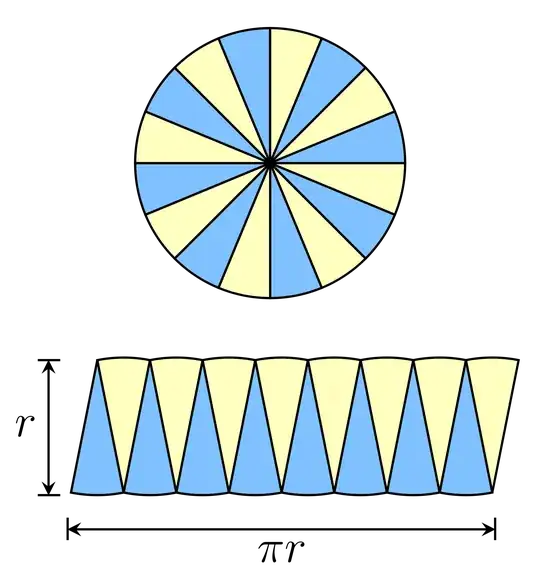
Here's a fun way to think of it. You know that the radius $r$ of a circle extends from the center of the circle to the edge of the circle. This gives an area of $A=\pi r^2$.

You also know that the area of a square is $A=s^2$ where $s$ is the length of the square's side. But what if we use a measurement of the square analogous to the radius of a circle? (Again, this is just for fun thinking...)

For the square, we'll let this new measurement extend from the square's center to the middle of one side. This is analogous to the radius of a circle (meaning it's comparable in certain respects, if we're mentally flexible). We could even call it $r$ if we want.

Since the length of a side $s$ of a square is equal to $2r$, we can say $s=2r$. This gives the square's area as $A=s^2=(2r)^2=4r^2$.

So, using our mental flexibility and analogous measurements of each object, we get the square's area as $A=4r^2$ and the circle's area as $A=\pi r^2$.

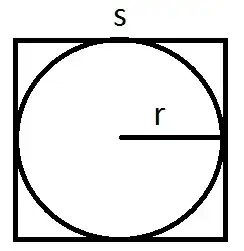
Now imagine we have a square and a circle, each with the same $r$. Let's let $r=1$. This gives the square's area as $A=4$ and the circle's area as $A=\pi =3.14159265358979323...$

This shows that, for the analogous $r$ measurement, the square's area is a little bigger than the corresponding circle. This makes sense if you look at the two figures. The square has 4 pointy corners that add this extra area.

Using our fun flexible measurements, we've supported what you believe: $r^2$ is a two dimensional measurement of area. For the circle (due to it's special shape) we multiply that two-dimensional measurement by the "conversion factor" of $\pi$ to get the final area. This conversion factor of $\pi$ is slightly less than what we'd have to multiply a square by ($4$) if we used a measurement of the square analogous to the radius of a circle.

Again, this was all for fun. People don't use $r$ to measure squares, but it would be cool if they did. There's so much more fun when you look into the wonders of this circular "conversion factor" $\pi$ and its amazing properties that extend well beyond circles. That's for another time though...

Answer 5

If I understand correctly you are asking how does $r\times r $ (the area of square) multiply by $\pi $ to make the area of a circle? Think: $$\begin {align}A&=\pi\times r^2\\&\approx3.14...\times r^2\\&\approx3r^2+0.1r^2+0.04r^2+...\end {align} $$

In other words you are summing smaller and smaller squares. These squares can be arranged to look ever more like the circle you want the area of.

Note $\pi$ has no dimension and $r $ has units of, for example, cm so the units are correct namely square cm.

There are issues of convergence I have hand waved a bit but I think this answers your question.

Hope this helps.

Answer 6

It seems like you are thinking about the ancient problem of "squaring the circle" that is, making a square with the same area as a given circle, the Greeks tried this for a long time and eventually found it to be impossible

Answer 7

What area is given by $\frac {r^2}{2}\sin \frac{2\pi}{n}$?

What area is given by $\frac {nr^2}{2}\sin \frac{2\pi}{n}$?

$$\frac {nr^2}{2}\sin \frac{2\pi}{n}=\frac{2\pi}{2\pi}\frac {nr^2}{2}\sin \frac{2\pi}{n}=\pi r^2\left(\frac{\sin \frac{2\pi}{n}}{\frac{2\pi}{n}}\right)$$ What is the limit of this when $n$ tends to infinity?

Answer 8

We know that if the area of a circle with radius 1 is $\pi$, then the area of a circle with any radius $r$ is $\pi r^2$ so it suffices to show that the the area of a circle with radius 1 is $\pi$. Here's a visual proof that the area of a circle with radius 1 is $\pi$.

Alternatively, you can prove that the area of any circle is $\pi r^2$ entirely by computing the definite integral $\int_{-r}^r 2\sqrt{r^2 - x^2} dx$ without even making the assumption that the area of any circle varies as the square of its radius. By using the substitution rule in reverse, you can compute that for any positive real number $r$, $\int_{-r}^r 2\sqrt{r^2 - x^2} dx = \int_{r \sin \frac{-\pi}{2}}^{r \sin \frac{\pi}{2}} 2\sqrt{r^2 - x^2} dx = \int_{r \sin \frac{-\pi}{2}}^{r \sin \frac{\pi}{2}}2r\cos(\sin^{-1}(\frac{x}{r})) dx = \int_{\frac{-\pi}{2}}^\frac{\pi}{2}2r\cos(x)\frac{d}{dx}(r \sin(x)) dx = \int_{\frac{-\pi}{2}}^\frac{\pi}{2}2r^2\cos^2(x) dx = \int_{\frac{-\pi}{2}}^\frac{\pi}{2}2r^2\frac{\cos(2x) + 1}{2} dx = \pi r^2$

Source: Area of a circle $\pi r^2$