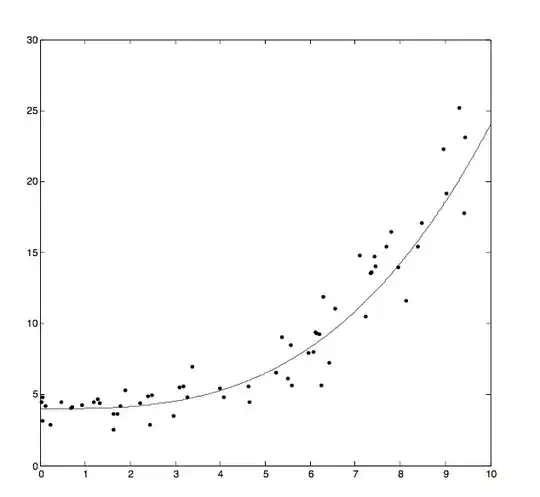
Given an exponential graph image of $f(x)$, how do you calculate $f(x)$?
Asked
Active
Viewed 316 times
2 Answers
0
If it is exponential then you can use the logarithms to fit a line since $\ln(e^x) = x$.
law-of-fives
- 1,963
-
Would you mind explaining through the calculation for me please? I know if y = Ae^bx that ln(y) = bx + ln(A) but I don't know how to calculate it from the graph! – Valentina May 01 '17 at 01:36
0
There are native ways to fit the function as noted in this posts. Logarithmic transformations will distort the problem.
Least squares solution for $y=ax^{b}$ after logarithmic transformation
Least Square Approximation for Exponential Functions
Suppose you want to use the functional form $y=ae^{bx}$.
From the boundary point $(0,4)$, we know $a=4$. Now solve for $b$ using the second endpoint $(10,24)$: $$ 4 e^{10b} = 24 $$ to find $$ b = \frac{\ln 6}{10} $$
dantopa
- 10,342
-
-
@Valentina: Do you have a functional form? Your plot provides some boundary points $(0,4)$, $(10,24)$. If you have an exponential form with two or three parameters you might make a decent guess. – dantopa May 01 '17 at 01:45
-
-
@Valentina: Readers are curious. Can you exactly state the question you were asked? Essential context seems absent. – dantopa May 01 '17 at 01:52
-
-
Excellent, thank you so much! This is exactly what I meant. My maths sucks so much now D: – Valentina May 01 '17 at 02:02
-
1"without using a calculator at all": are you kidding ? This is not humanly doable by hand. – May 19 '17 at 10:16