5

This is an exercise from Stefan Heinz Mathematical Modeling:

enter image description here

Linearizing $y=ax^b$ is very easy applying log in both sides. But when the constant $c$ appears here I would get $\ln(y-c)=\ln a + b\ln x$. The constant $c$ is to be determined but it appears inside a log so $\ln(y-c)$ can't be derived from the data and therefore I can't test the suitability of the assumption (in order to do this, I have to plot $\ln(y-c)$ vs $\ln x$). I am very confused by what am I supposed to do in this exercise.

Lotte
  • 1,070
  • 1
    Perhaps the point is that since $y$ is increasing we must have $ax^b$ increasing too. Thus $a\cdot0^b=0$ and therefore $c=y(x=0)\approx100$. So maybe it is safe to assume $c=100$? – String Sep 25 '16 at 21:26
  • $y(0)=c$ by substitution, $y(0)=100$ by the table, so $c=100$ by transitive property. – Alex Jones Apr 09 '17 at 01:40

1 Answers1

2

Least squares solution

Start with data set $m=5$ points, $$\left\{ x_{k}, y_{k} \right\}_{k=1}^{m}$$ Model function $$ y(x) = a x^{b} - c. $$ Define least squares solution: $$ (a,b,c)_{LS} = \left\{ (a,b,c) \in \mathbb{C}^{3} \colon \sum_{k=1}^{m} \left( y_{k} - a x_{k}^{b} - c \right)^{2} \text{ is minimized} \right\} $$ Compute least squares solution: $$ \begin{align} a_{LS} &= 0.6947372490916177, \\ b_{LS} &= 3.6934462148212246, \\ c_{LS} &= 100.57131353798891. 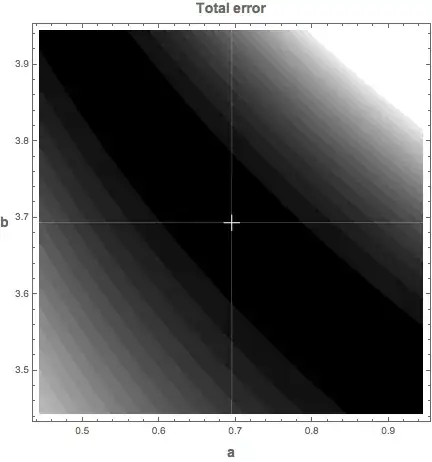\end{align} $$ Total error: $$ r^{2} \left( a_{LS}, b_{LS}, c_{LS} \right) = \sum_{k=1}^{m} \left( y_{k} - a_{LS} x_{k}^{b_{LS}} - c_{LS} \right)^{2} = 0.694737 $$ The total error function $r^{2}\left( a, b, c_{LS} \right)$ is plotted below, with the white dot showing the least squares solution.

merit

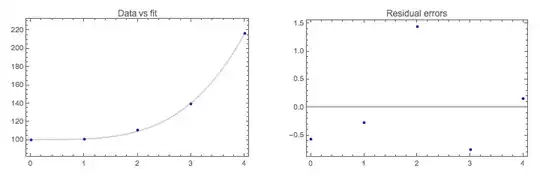
The data points, the predictions, and the residual errors are listed and plotted below. The total error is $$r^{2} = 3.06477$$.

$$ \begin{array}{crll} x_{k} & y_{k} & \phantom{w}y(x_{k}) & \phantom{www}r_{k}\\\hline 0 & 100 & 100.571 & -0.571314 \\ 1 & 101 & 101.266 & -0.266051 \\ 2 & 111 & 109.559 & \phantom{-}1.44078 \\ 3 & 140 & 140.754 & -0.754306 \\ 4 & 217 & 216.849 & \phantom{-}0.150893 \\ \end{array} $$

residuals

Logarithmic transformation

Logarithmic transformations distort the problem. The solution that follows is not the solution of the original problem (For example, Least Square Approximation for Exponential Functions). This will be more clear when we compare the total errors.

The problem to solve $$ \begin{align} y - c = ax^{b} \end{align} $$ is replaced with this problem $$ \begin{align} \ln (y - c) &= \ln \left(ax^{b}\right) \\ &= \ln a + b \ln x \end{align} $$ The logarithmic transformation is an exact map when there is no error. But the fact we resort to least squares is an admission of existence of error. So the transformation only works in the case where we don't use it.

The input data is \begin{array}{ll} x & y \\\hline 0 & 0 \\ \ln (2) & \ln (11) \\ \ln (3) & \ln (40) \\ \ln (4) & \ln (117) \\ \end{array}

The outputs are $$ \ln a = 0.0031410142182181078 \qquad \Rightarrow \qquad a = 1.0031459523722948, $$ and $$ b = 3.4097548950738794. $$

Total error for the transformed problem is $$ r^{2} = 19.956 $$

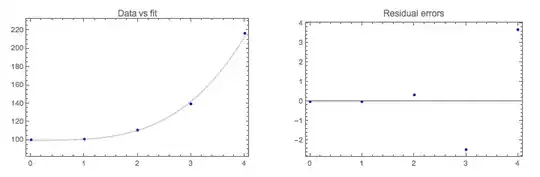
The data, predictions and residual errors are tabulated and plotted below. $$ \begin{array}{crll} x_{k} & y_{k}\phantom{w} & \phantom{w}y(x_{k}) & \phantom{www}r_{k}\\\hline 0. & 100. & 100. & \phantom{-}0. \\ 1. & 101. & 101.003 & -0.00314595 \\ 2. & 111. & 110.661 & \phantom{-}0.338885 \\ 3. & 140. & 142.485 & -2.48451 \\ 4. & 217. & 213.303 & \phantom{-}3.69707 \\ \end{array} $$

Note the larger size of the residuals compared to the original fit.

log

The doubling value in part (d) is found by solving $$ ax^{b} = 100 \qquad \Rightarrow \qquad x= 3.85614 $$

dantopa
  • 10,342