In which cases do multiple hyperbola branches have two intersection points?

Question

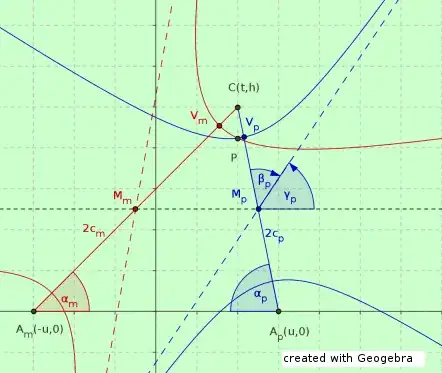
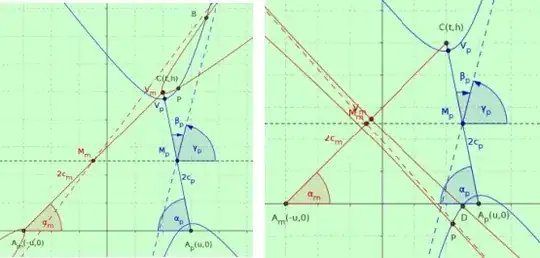
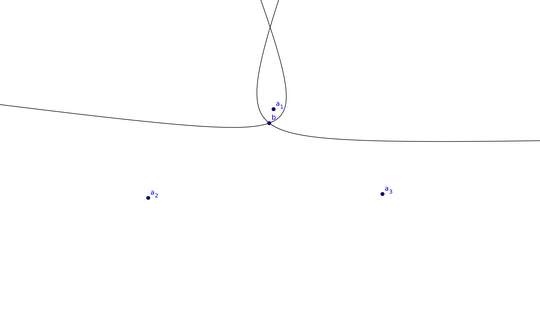
I am researching on hyperbolic localization techniques. In these techniques there are usually three anchor nodes $a_1, a_2$ and $a_3$ trying to position a blind node $b$. To do this, hyperbola branches are estimated which pass through the blind node and have the anchor nodes as foci. The position is then estimated as the intersection point of these hyperbola branches.

Image: Two hyperbola branches. Both passing through the blind node, one using $a_1$ and $a_2$ as foci, the other using $a_1$ and $a_3$.

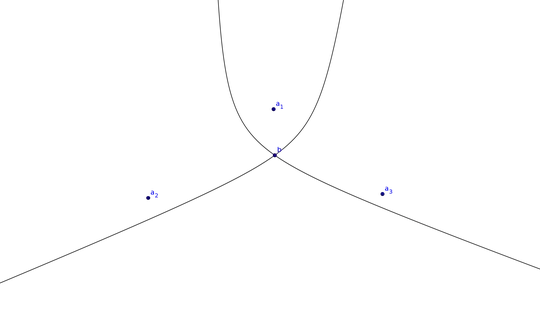
However, hyperbola branches can have two intersection points. I am trying to understand, for which positions of the blind node, relative to the anchor nodes, there are two intersection points.

Image: The same scenario as before, but a different position of the blind node. The hyperbolas intersect in two points.

I have seen this figure in an academic paper, where the areas were colored, which lead to two intersection points, if the blind node falls in one of these areas:

My goal is to create such figures myself. Therefore I have to understand the mathematical relation.

In this figure, for each anchor node, there is one such area, constraint by a hyperbola branch. Appearently this hyperbola branch has as foci: the respective anchor node and the anchor node mirrored on the midpoint between the other two anchor nodes. But I do not know how to determine the semi-axis $a$.

I am happy for any suggestions.

Answer 1

Without loosing in generality we can place two anchor nodes ($A_m$ and $A_p$) symmetrically on the $x$ axis , and place the third ($C$) in the upper half-plane as shown in the scheme above.

Let's consider the localization effectuated by node $C$ respectively with nodes $A_m$ and $A_p$, by crossing the red and blue hyperbolich branches at point P.
Denote as $2c_m$ and $2c_p$ the distances from node $C$ to the other nodes, and as $M_m$ and $M_p$ the middle points of the connecting segments.
Clearly the hyperbolas will be centered on such midlle-points, and will have linear eccentricity (distance center to focus) equal to $c_m$, $c_p$.
Let's call $a_m$ and $a_p$ the semiaxes from center to vertices (the measured differences in distance).

We can deduct, from the figure and the properties of hyperbola, that the branches will intersect "properly" iff the respective asymptotes are "interleaved", i.e. if their points at infinite alternates (one "red", one "blue", ..). That can be better figured by noting the "improper" situations below.

Now it is known that the angle that the asymptotes make with the hyperbola axis, the angles $\beta$ in the pictures, are given by $$ \beta = \arctan \left( {\sqrt {\left( {\frac{c}{a}} \right)^{\,2} - 1} } \right) $$ The angles $\alpha$ made by the axis with the horizontal line are determined from the positioning of the nodes.
So, with the notations in the figure, the angles $\gamma$ between the asymptotes and the $x$ axis will be: $$ \begin{array}{l} \gamma _{\,m} = \alpha _{\,m} \pm \beta _{\,m} = \alpha _{\,m} \pm \arctan \left( {\sqrt {\left( {\frac{{c_{\,m} }}{{a_{\,m} }}} \right)^{\,2} - 1} } \right) \\ \gamma _{\,p} = \pi - \alpha _{\,p} \pm \beta _{\,p} = \pi - \alpha _{\,p} \pm \arctan \left( {\sqrt {\left( {\frac{{c_{\,p} }}{{a_{\,p} }}} \right)^{\,2} - 1} } \right) \\ \end{array} $$ Therefore we shall ensure that $$ \gamma _{\,m\, - } < \gamma _{\,p\, - } < \gamma _{\,m\, + } < \gamma _{\,p\, + } $$ i.e. $$ \bbox[lightyellow] { \left\{ \begin{array}{l} 0 < \beta _{\,p} ,\beta _{\,m} < \pi /2 \\ - \alpha _{\,c} < \beta _{\,p} - \beta _{\,m} < \alpha _{\,c} \\ \alpha _{\,c} < \beta _{\,m} + \beta _{\,p} \left( { < \pi } \right) \\ \end{array} \right.\quad \left| {\;\alpha _{\,c} = \pi - \alpha _{\,p} - \alpha _{\,m} } \right. } $$ where $\alpha _{\,c} $ is thus the angle in $C$.
The set of inequalities is rendered graphically as below.

From here it is just a computational task to deduce the bounds for $a_m$ and $a_p$ and from these, which are the differences between the distances from $C$ and from the other nodes, the boundary positions of the detectable point $P$.