1

Given two hyperbolas h1(with foci and center) and h2(with foci and center), In what condition these hyperbolas will not intersect to each other?. I can get the condition when h1 and h2 are standard hyperbola (parallel to axis and the center is the origin). I want to find the condition when both of them are not standard hyperbola. Thanks

a hidayat
  • 31
  • I think you ask a too general question. You should for example restrict your attention to equilateral hyperbolas and take one of them as the standard equilateral hyperbola with equation $xy=1$ and the other one as a rotated + translated image of the first one. Besides, do you know the focal definition $|MF-MF'| \ = \ $constant of a hyperbola ? – Jean Marie Feb 16 '17 at 10:22
  • @JeanMarie. Thanks and apologize for unclear question. This question is for equilateral hyperbola. I know that constant property of hyperbola – a hidayat Feb 16 '17 at 10:29

3 Answers3

2

Let $x^2-y^2=1$ be the first hyperbola.

  • Re-scaling $$x^2-y^2=c^2 \tag{$c^2 \ne 1$}$$

  • Conjugate $$y^2-x^2=c^2$$

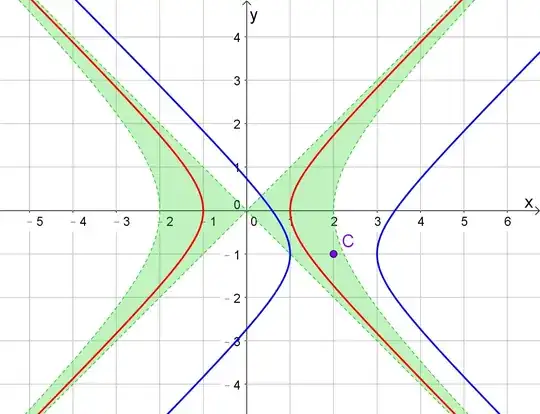
  • Translation \begin{align*} (x-h)^2-(y-k)^2 &= 1 \\ 2(ky-hx)+h^2-k^2 &= 0 \\ x &= \frac{h^2-k^2+2ky}{2h} \\ (h^2-k^2+2ky)^2-4h^2 y^2 &= 4h^2 \\ 4(h^2-k^2)y^2-4k(h^2-k^2)y+4h^2-(h^2-k^2)^2 &= 0 \\ \Delta & < 0 \\ k^2(h^2-k^2)^2-(h^2-k^2)[4h^2-(h^2-k^2)^2] & < 0 \\ h^2(h^2-k^2)(h^2-k^2-4) &< 0 \\ \end{align*}

$$\fbox{$0<h^2-k^2<4$}$$

enter image description here

Ng Chung Tak
  • 18,990
  • Thanks. I still don't get the second line (before x=......). Where are x^2 and y^2 go, they suddenly disappear. – a hidayat Feb 17 '17 at 08:26
  • Equating $x^2-y^2=(x-h)^2-(y-k)^2=1$, all quadratic terms have gone. Then substitute either back into either hyperbola. – Ng Chung Tak Feb 17 '17 at 12:02
  • [+1] Good treatment of the condition $0<h^2-k^2<4$ with a nice drawing giving a geometrical understanding. It remains to show that, if there is a rotation, whatever the translation, there are necessarily intersection points. I think I have a proof now. I will write it in the coming hours. – Jean Marie Feb 18 '17 at 18:18
  • In general, if conic $ax^2+bxy+cy^2=1$ is translated by $(h,k)$ such that they don't intersect, then $$(b^2-4ac)(ah^2+bhk+ck^2)(ah^2+bhk+ck^2-4)<0$$ – Ng Chung Tak Feb 18 '17 at 20:55
  • In general hyperbola equation ax^2+bxy+cy^2=1. Are a, b and c here similar with a,b,c in standard hyperbola equation x^2/a^2 - y^2/b^2 = 1, where a^2+b^2 = c^2? Thanks – a hidayat Feb 20 '17 at 01:21
  • No, it's general form for central conics. Some texts may write it in quadratic form: $$\begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix} a & \frac{b}{2} \ \frac{b}{2} & c \end{pmatrix} \begin{pmatrix} x \ y \end{pmatrix}=1$$ – Ng Chung Tak Feb 20 '17 at 11:06
0

use the answer of this question to get two equations, set them inequal to each other, then that is your condition, swap them back to focal model.

PS: it might be easier to answer in polar or bipolar coordinates, as they seem more suitable for parabola solving problems

Community
  • 1
jimjim
  • 9,675
0

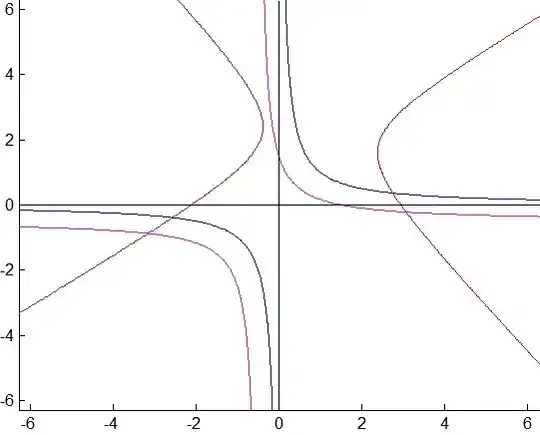
Let us consider the reference equilateral hyperbola with equation $xy=1$ (see blue curve on graphics below). Any rectangular hyperbola can be obtained from the reference with a rotation (angle $\theta$) followed by a translation (vector $\binom{a}{b}$). One should obtain the following result :

  • if $\theta\neq0$, there are intersection points.

  • If $\theta=0$, the only translations that give no intersection point are with vector $k\binom{1}{1}$ for $-2<k<2$ (see the example of the magenta curve).

I thought I have a proof but it is not the case.

enter image description here

Jean Marie
  • 81,803