Do Hermite polynomials exist for negative integers?

Question

I recently asked a question about a differential equation, and received this as an answer. It included a Hermite polynomial of negative degree, namely $H_{-3}$. I searched online and it seems as though these $H_n$'s are only defined for $n\ge0$, and for $n<0$ something else might used - parabolic cylinder functions. I say 'might' because I am not sure if they are actually the same. I have never heard of these, and so was hoping someone would know about them here. Can they be expressed in terms of erf or erfc? I found another link which suggested they could. If so, how?

To clarify I want to know if Hermite polynomials (or their equivalent) can be expressed for negative integers $n$ in some closed form expression (including erf).

Answer 1

As I added to my answer to the previous question.

Expanded using more usual functions, $$H_{-3}\left(\frac{x}{2}\right)=\frac{1}{16} \left(\sqrt{\pi } e^{\frac{x^2}{4}} \left(x^2+2\right) \text{erfc}\left(\frac{x}{2}\right)-2 x\right)$$

Similarly,$$H_{-1}\left({x}\right)=\frac{1}{2} \sqrt{\pi } e^{x^2} \text{erfc}(x)$$ $$H_{-2}\left({x}\right)=\frac{1}{2} \left(1-\sqrt{\pi } e^{x^2} x \text{erfc}(x)\right)$$ $$H_{-3}\left({x}\right)=\frac{1}{8} \left(\sqrt{\pi } e^{x^2} \left(2 x^2+1\right) \text{erfc}(x)-2 x\right)$$ $$H_{-4}\left({x}\right)=\frac{1}{24} \left(2 \left(x^2+1\right)-\sqrt{\pi } e^{x^2} x \left(2 x^2+3\right) \text{erfc}(x)\right)$$ $$H_{-5}\left({x}\right)=\frac{1}{192} \left(\sqrt{\pi } e^{x^2} \left(4 \left(x^2+3\right) x^2+3\right) \text{erfc}(x)-2 x \left(2 x^2+5\right)\right)$$

Answer 2

After two days of thinking about this, I see now how Hermite polynomials can be extended to negative indices from a more basic approach. I was inspired to do this because you can't argue with Claude's result. So let's return to the Rodriques formula,

$$\text{H}_n(x)=(-)^n e^{x^2} \frac{d^n}{dx^n}e^{-x^2}$$

Thinking in terms of fractional calculus, I'm going to stretch the imagination and allow for differintegration with negative $n$. Thus we boldly say that

$$\text{H}_{-1}(x)=-e^{x^2} \int e^{-x^2} dx=\frac{\sqrt{\pi}}{2} e^{x^2}\text{erfx}(x)$$

This is in agreement with Claude's result. At this point we can continue with the recursion formula since we know that $H_0=1$. Thus, working down the negative numbers,

$$\text{H}_n(x)=\frac{1}{2(n+1)}\left[2\text{H}_{n+1}(x)-\text{H}_{n+2}(x)\right],\ \ \ \ n<-1$$

Obviously, these are not polynomials, but they derive from the Hermite polynomial recursion so that's what we call it. These look much different than the regular Hermite polynomials.

The figure below show the first eight $H_n, n\le -1$. Notice the logarithmic $y$-axis.

Answer 3

I'm looking at K. Oldham, J. Myland, & J. Spanier, An Atlas of Functions, Ch. 24, Springer, and I see no mention of negative $n$ for the Hermite polynomials. Moreover, a Rodrigues's formula seems to rule it out altogether,

$$\text{H}_n(x)=(-)^ne^{x^2}\frac{d^n}{dx^n}e^{-x^2}$$

On the other hand, the integral representation does not seem so prejudiced,

$$\text{H}_n(x)=\frac{2^{n+1}e^{x^2}}{\sqrt{\pi}}\int_0^{\infty}t^ne^{-t^2}cos\left(2xt-\frac{n\pi}{2}\right)dt$$

But again, there is no mention of negative $n$ in that chapter. In addition is stated clearly that the Hermite polynomials are a special case of the parabolic cylinder function, whose order $\nu$ is a nonnegative integer $n$ and is given by

$$\text{D}_n(x)=2^{-n/2}e^{-x^2/4}\text{H}_n\left(\frac{x}{\sqrt{2}}\right)$$

I don't see any reference to the error function.

UPDATE: I found the following relation with respect to the error function in Olver, et al., NIST Handbook of Mathematical Functions,

$$\frac{d^{n+1}\text{erf}\ z}{dz^n}=(-1)^n\frac{2}{\sqrt{\pi}}\text{H}_n(z) e^{-z^2}, \ \ \ \ n=0,1,2,\ ...$$

Answer 4

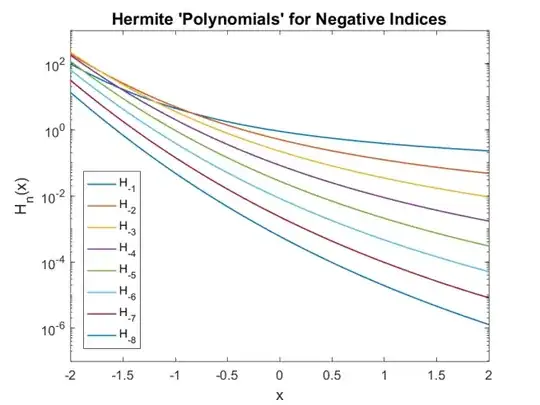
Take $n \in {\mathbb N}$ and $n \ge 1$. By generalizing the Rodrigues's formula to negative values of $n$ we write:

\begin{eqnarray} &&H_{-n}(x) := (-1)^{n+1} e^{x^2} \cdot \int\limits_x^\infty \frac{(x-t)^{n-1}}{(n-1)!} e^{-t^2} dt \\ &&= \frac{(-1)^{n-1}}{(n-1)!} \frac{1}{2} \sum\limits_{j=0}^{n-1} \sum\limits_{m=0}^{\lfloor \frac{j}{2} \rfloor} \binom{n-1}{j} x^{n-1-j} (-1)^j (\frac{j-1}{2})_{(m)} \left( \right. \\ && \left. x^{j-1-2 m} 1_{m < \lfloor \frac{j}{2} \rfloor} + [1 \cdot 1_{j\%2=1} + \sqrt{\pi} e^{x^2} \mbox{erfc}(x) 1_{j\%2=0}] 1_{m = \lfloor \frac{j}{2} \rfloor} \right. \\ && \left. \right) \\ &&=\frac{(-1)^{n-1}}{2(n-1)!}\underline{\sum\limits_{j=0}^{\lfloor \frac{n-2}{2} \rfloor} \left(j!\sum\limits_{m=2j+1}^{n-1}\binom{n-1}{m} (-1)^m \binom{\frac{m-1}{2}}{j}\right) x^{n-2-2j}} + \\ &&\frac{(-1)^{n-1}}{2(n-1)!}\underline{\sum\limits_{j=0}^{\lfloor \frac{n-1}{2} \rfloor} \binom{n-1}{2 j} \cdot (\frac{1}{2})^{(j)} x^{n-1-2 j} }\cdot \sqrt{\pi} e^{x^2} \mbox{erfc}(x) \end{eqnarray} where $j_{(m)} := j(j-1)\cdots(j-m+1)$ is the lower Pochhammer symbol.

In[243]:= x =.; mm = 20;
Table[(-1)^(n - 1)/(n - 1)! 1/2 Sum[
      Binomial[n - 1, j] x^(n - 1 - j) (-1)^
        j Pochhammer[(j - 1)/2 - m + 1, m] If[m < Floor[j/2], 
        x^(j - 1 - 2 m), 
        If[Mod[j, 2] == 1, 1, Sqrt[\[Pi]] E^x^2 Erfc[x]]], {j, 0, 
       n - 1}, {m, 0, Floor[j/2]}] - HermiteH[-n, x], {n, 1, mm}] // 
  FunctionExpand // Simplify
Table[ (-1)^(-1 + n)/(2 (-1 + n)!)
      Sum[(Sum[
          Binomial[n - 1, m] (-1)^m Binomial[(m - 1)/2, j], {m, 
           2 j + 1, n - 1}] j!) x^(n - 2 - 2 j), {j, 0, 
       Floor[(n - 2)/2]}] + (-1)^(-1 + n)/(2 (-1 + n)!)
      Sum[Binomial[n - 1, 2 j + 0]  Pochhammer[1/2, 
        j] x^(n - 1 - 2 j) , {j, 0, Floor[(n - 1)/2]}] Sqrt[\[Pi]] E^
      x^2 Erfc[x] +
    -HermiteH[-n, x]
   , {n, 1, mm}] // FunctionExpand // Simplify
Out[244]= {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}
Out[245]= {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}

It turns out that those quantities appear in a natural way in stochastic processes, in the formula for the probability density function of the first hitting time of a certain diffusion process, as demonstrated in my answer to this question.