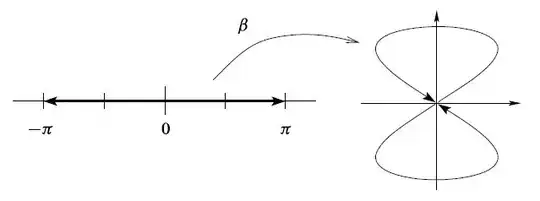
On page 86 of John Lee's Introduction to smooth manifolds there is an example of an injective immersion that is not a topological embedding:
$\beta : (-\pi, \pi) \to \mathbb{R}^2$, defined by $\beta(t) = (\sin{2t}, \sin{t})$, or pictorially:
It is explained that, although $\beta$ is an injective immersion, it is not a smooth embedding since the image is compact while the domain is not. My understanding is that the image, while bounded in $\mathbb{R}^2$, is an open subset of the plane, whereas the statement claims that it is not.
Would anyone please explain why the image is compact? Thank you.