0

I understand generally that embeddings are injective maps which are homeomorphic to their immage and that immersions are local embeddings but i fail to see the distinction of precisely why this is the case and why a figure of eight linesegment (immersed via the map $t\mapsto(\cos(\pi/2+t),\sin(2t))$ for $0<t<2\pi$) can be immersed into $\mathbb{R}^2$ but not embedded. I haven't been able to find a mathematical proof of why the crossing point is not homeomorphic and secondly from the definiton of immersion: "A surface is immersed if every point of the domain has a neighborhood which is embedded by the map." What defines how big the neighborhood is and does every point in there need to be embedded, excluding the point itself, or just any for it to be an immersion.

As I understand injective, every point of the domain needs to be mapped to a unique point in the co-domain but how does this work for the crossing point as there are two values of $t$ whch map to identical points in $\mathbb{R}^2$ ($\pi/2$ and $3\pi/2$)

Paul Frost
  • 76,394
  • 12
  • 43
  • 125
Sebastien Bienfait
  • 37
  • 2
  • Sebastian, I fixed up the mathjax in your question. Please check to make sure I got everything right. Have you tried searching MSE for your question? It seems to be fairly common (e.g.). – Tyrone Dec 04 '20 at 19:07
  • One easy way to see that the map is not an embedding (subspace toplogy on $\mathbb R^2$) is to note that the figure eight is compact but $(0,2\pi)$ is not. – Matematleta Dec 04 '20 at 19:51

1 Answers1

2

Why can a figure eight, immersed in $\Bbb R^2$ via $t\mapsto \left(\cos\left(\frac\pi 2+t\right),\sin(2t)\right)$, be immersed in $\Bbb R^2$ but not embedded?

You need to first state what the figure eight is. To talk about immersions, you should have a map between smooth manifolds, but the figure eight with a crossing is not a smooth manifold. If the figure eight means a copy of $S^1$ with a twist, then this is diffeomorphic to $S^1$ and can certainly be embedded in $\Bbb R^2$. However, this depends entirely on the map used. It does not make sense to ask if something immersed in $\Bbb R^2$ can be embedded in $\Bbb R^2$. You can either ask if one manifold can be embedded in another, or if a given map between manifolds is an embedding.

Again, as a smooth manifold, the figure eight is just $S^1$, so we need to specify a map $f\colon S^1\to \Bbb R^2$. Really, we want to imagine first embedding $S^1$ into $\Bbb R^3$ so that it looks like a figure eight from above. Here is an example, where $S^1$ is shown as a tube for the sake of visualizing.

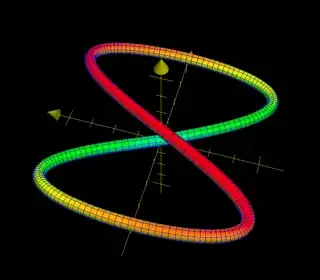
a fattened embedding of S^1 in R^3

Now if we project down to the $xy$ plane, we get a map $S^1\to \Bbb R^2$ whose image is shown below.

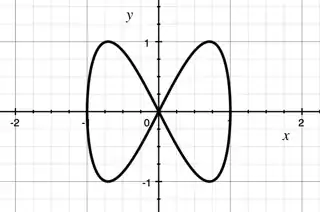
the image of an immersion of S^1 in R^2

One can show that this is an immersion, meaning that for any $p\in S^1$, the differential map $df_p\colon T_pS^1\to T_{f(p)}\Bbb R^2$ is injective. However, $f$ itself is not even injective! There are clearly two points in $S^1$ which both land on the origin in $\Bbb R^2$. So $f$ is not a bijection onto its image, and therefore not a homeomorphism onto its image (embedding).

I haven't been able to find a mathematical proof of why the crossing point is not homeomorphic.

This language doesn't make sense, but you probably mean the following: for any open set $U\subset\Bbb R^2$ containing the origin, there is no homeomorphism between $U\cap f(S^1)$ and a neighborhood of $S^1$. This is more difficult to prove; I would probably use algebraic topology.

To summarize, there are distinct questions one could ask here:

  1. Is there an embedding $S^1\to \Bbb R^2$? (Yes.)
  2. Is the map $f\colon S^1\to \Bbb R^2$ an embedding? (No because $f$ is not injective.)
  3. Is there an embedding from $S^1$ to $f(S^1)$ (topologized as a subset of $\Bbb R^2$)? (No but this is less immediate.)
pancini
  • 19,216
  • thank you for your answer. So for the immersion, the map itself doesnt need to be injective, rather the df_p map needs to be injective? and because the map f isnt injective, its not an embedding? – Sebastien Bienfait Dec 05 '20 at 13:58
  • 1
    That's right, immersions need not be injective. However, there are, in fact, injective immersions that are not embeddings. You have to try a bit harder to find instances of this, but you can see some if you search SE. – pancini Dec 05 '20 at 19:07
  • One example is $\Bbb R$ mapped into $\Bbb R^2$ so that it curls back toward itself in a smooth P-shape. It never quite makes contact with itself, so the map is still injective. It is also an immersion, but not an embedding. – pancini Dec 05 '20 at 19:12