69

Playing around on wolframalpha shows $\tan^{-1}(1)+\tan^{-1}(2)+\tan^{-1}(3)=\pi$. I know $\tan^{-1}(1)=\pi/4$, but how could you compute that $\tan^{-1}(2)+\tan^{-1}(3)=\frac{3}{4}\pi$ to get this result?

Clayton Kershaw
  • 693
  • 2
    It is true in general that $\tan^{-1}(a) + \tan^{-1}(b) + \tan^{-1}(c) = \pi$ when $a+b+c=abc$ (and $a,b,c$ positive). This is the converse of what is proved here. – hmakholm left over Monica Oct 19 '15 at 11:55
  • That generalization is so cool! Of course, for positive integers a, b, c, the only solution to a+b+c = abc (not counting permutations of a,b,c) is 1, 2, 3. Just around 2001 I had connected the two topics (the trig identity and sum = product) without realizing this generalization, perhaps because I was sticking to integers. See: Michael W. Ecker, When Does A Sum Of Positive Integers Equal Their Product?, Mathematics Magazine, February 2002, Vol. 75, No. 1, p. 41-47. – Dr. Michael W. Ecker Jan 10 '24 at 19:14

7 Answers7

92

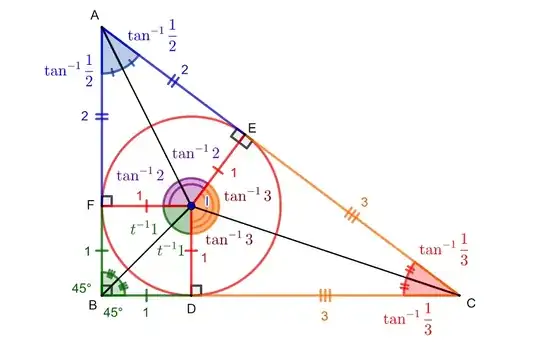
enter image description here

Consider $O=(0,0)$, $A=(1,1)$, $B=(-1,3)$, $D=(1,-3)$, $E=(1,0)$.

\begin{align} 2 &= \frac{AB}{AO} = \tan \angle AOB \\ 1 &= \frac{AE}{EO} = \tan \angle AOE \\ 3 &= \frac{DE}{DO} = \tan \angle DOE \end{align}

The points B, O and D are collinear, i.e. $\angle BOD = \tan^{-1}2+\tan^{-1}1+\tan^{-1}3 = \pi$.

kennytm
  • 7,495
69

Proof without word

$\tan^{-1} 1+\tan^{-1} 2+\tan^{-1} 3 =\pi$.

JSCB
  • 13,456
  • 15
  • 59
  • 123
60

The simplest way is by using complex numbers. It is a trivial computation to show that $$(1+i)(1+2i)(1+3i)=-10$$ Now recall the geometric description of complex multiplication (multiply the lengths and add the angles), and take the argument on both sides of this equation. This gives $$\tan^{-1}(1)+\tan^{-1}(2)+\tan^{-1}(3)=\pi$$

Per Erik Manne
  • 11,106
38

$$\tan^{-1}(2)+\tan^{-1}(3)=\tan^{-1}{\left(\frac{2+3}{1-2\cdot 3}\right)}=\tan^{-1}(-1)=n\pi-\frac \pi 4,$$ where $n$ is any integer.

Now the principal value of $\tan^{-1}(x)$ lies in $[-\frac \pi 2, \frac \pi 2]$ precisely in $(0, \frac \pi 2)$ if finite $x>0$. So, the principal value of $\tan^{-1}(2)+\tan^{-1}(3)$ will lie in $(0, \pi) $.

So, the principal value of $\tan^{-1}(2)+\tan^{-1}(3)$ will be $\frac {3\pi} 4$.

Interestingly, the principal value of $\tan^{-1}(-1)$ is $-\frac {\pi} 4$.

But the general values of $\tan^{-1}(2)+\tan^{-1}(3)$ and $\tan^{-1}(-1)$ are same.

Alternatively, $$\tan^{-1}(1)+\tan^{-1}(2)+\tan^{-1}(3)=\tan^{-1}{\left(\frac{1+2+3-1\cdot 2\cdot 3}{1-1\cdot 2- 2\cdot 3 -3\cdot 1}\right)}=\tan^{-1}(0)=m\pi$$, where $m$ is any integer.

Now the principal value of $\tan^{-1}(1)+\tan^{-1}(2)+\tan^{-1}(3)$ will lie in $(0 ,\frac {3\pi} 2)$ which is $\pi$.

The principal value of $\tan^{-1}(0)$ is $0\neq \pi$.

Ahaan S. Rungta
  • 7,706
lab bhattacharjee
  • 274,582
13

Note that $$ \tan \left(\arctan(1+z) + \arctan\left(2 + z + z^2 \right) + \arctan \left( 3+3\,z+4\,{z}^{2}+2\,{z}^{3}+{z}^{4} \right) \right)=z $$ so that $$\arctan(1+z) + \arctan\left(2 + z + z^2 \right) + \arctan \left( 3+3\,z+4\,{z}^{2}+2\,{z}^{3}+{z}^{4} \right) = \arctan(z) + n \pi $$ for the appropriate integer $n$. For integers $z$ we get interesting arctan identities from this.

$$\eqalign{ \arctan(1) + \arctan\left(2\right)+ \arctan\left(3\right) &= \pi \cr \arctan(2) + \arctan(4) + \arctan(13) &= \arctan(1) + \pi \cr \arctan(3) + \arctan(8) + \arctan(57) &= \arctan(2) + \pi \cr \arctan(4) + \arctan(14) + \arctan(183) &= \arctan(3) + \pi \cr}$$ etc.

JSCB
  • 13,456
  • 15
  • 59
  • 123
Robert Israel
  • 448,999
  • 2
    How did you manage the first equation? – Nastassja Sep 16 '12 at 07:09
  • 3
    I asked Maple for integer solutions of $$\frac{a+b+c-abc}{1-ab-bc-ca} = d$$ – Robert Israel Sep 16 '12 at 07:24
  • I know that this an old answer, but would you please explain how the integer solutions of $$\frac{a+b+c-abc}{1-ab-bc-ca} = d$$ relate to your first identity? I can't see it on my own :( – math.n00b Jul 23 '14 at 09:58
  • Maple gave me a parametric solution which simplifies to $$\left{ a={{\it _Z1}}^{4}+2,{{\it _Z1}}^{3}+4,{{\it _Z1}}^{2}+3 ,{\it _Z1}+3,b={{\it _Z1}}^{2}+{\it _Z1}+2,c=1+{\it _Z1},d={\it _Z1} \right} $$ – Robert Israel Jul 23 '14 at 15:12
  • @math.n00b $\tan(\arctan(a)+\arctan(b)+\arctan(c)) = ?$ – Max Payne Nov 05 '16 at 07:18
0

Consider, $z_1= \frac{1+2i}{\sqrt{5}}$, $z_2= \frac{1+3i}{\sqrt{10} }$, and $z_3= \frac{1+i}{\sqrt{2} }$, then:

$$ z_1 z_2 z_3 = \frac{1}{10} (1+2i)(1+3i)(1+i)=-1 $$

Take arg of both sides and use property that $\arg(z_1 z_2 z_3) = \arg(z_1) + \arg(z_2) + \arg(z_3)$:

$$ \arg(z_1) + \arg(z_2) + \arg(z_3) = -1$$

The LHS we can write as:

$$ \tan^{-1} ( \frac{2}{1}) +\tan^{-1} ( \frac{3}{1} ) + \tan^{-1} (1) = \pi$$

Tl;dr: Complex number multiplication corresponds to tangent angle addition

tryst with freedom
  • 11,538
0

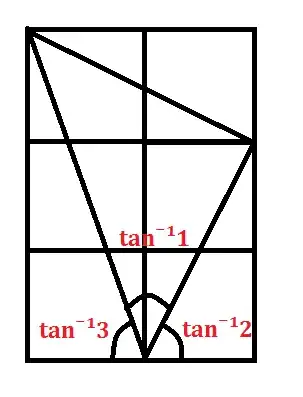
I would like to add this relatively less known proof without words of following two identities in the diagram below.

  1. $$\tan^{-1} 1 + \tan^{-1} 2 + \tan^{-1} 3 = \pi$$
  2. $$\tan^{-1} \frac{1}{2} + \tan^{-1} \frac{1}{3} = \frac{\pi}{4}$$

enter image description here

MyMolecules
  • 3,823