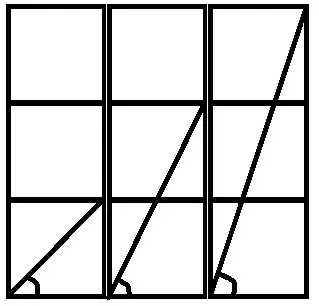
I know this is easy to lots of you but I am just struggling to find the solution. How can I prove the sum of the highlighted angles in the following 3 times 3 square grid is equal to $\pi$?
Asked
Active
Viewed 267 times
3
-
4Answers here and here. – dtldarek Jan 01 '17 at 21:24
-
Cool, feel free to mark as duplicated. Thanks! – kchpchan Jan 01 '17 at 22:13
-
This is a question from Brilliant. Brilliant problems cannot be discussed or solved anywhere else. – Soha Farhin Pine Jan 02 '17 at 20:13
3 Answers
3
Hint: Apply the arctan addition formula to angles $\arctan(1), \arctan(2), \arctan(3)$.
John Hughes
- 93,729
2
Here's a fun little proof without words. Sorry for the horrible art skills.
0
The first angle is $\pi /4$ because his tangent is equal to $1$ so we must show that $a+b=3\pi /4$. Looking to the picture we have $\tan a= 2$ and $\tan b= 3$ so:
$$\tan(a+b)=\frac{\tan a + \tan b}{1-\tan a \tan b}=\frac{2+3}{1-2\cdot3}=-1$$
and once $a+b \le \pi$ then $a+b=3\pi /4$.
John Hughes
- 93,729
Arnaldo
- 21,342