$$\sin x + \cos x = \sqrt{2} \sin(x + \pi/4)$$
Is there an easy way to visualize this identity or to convert the left-hand side to the right-hand side?
In general, can $p \sin x + q \cos x$ for some integers $p$ and $q$ be easily expressed as $\sin($something$)$ or $\cos($something$)$? If so, how can that be done?
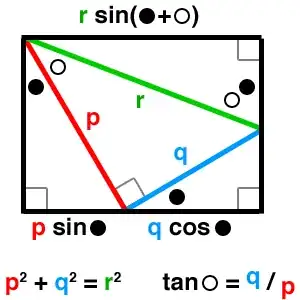
Intuitive visualization:
The sine of $t$ is the $y$ coordinate of an initially horizontal unit vector as it rotates counterclockwise by $t$ radians about the origin.
The cosine of $t$ is the $y$ coordinate of an initially vertical unit vector at it rotates counterclockwise by $t$ radians about the origin.
Then $\sin t+\cos t$ is the $y$ coordinate about the shown sum of the horizontal and vertial unit vectors as the whole diagram rotates counterclockwise by $t$ radians about the origin.
But that is the same as rotating the dotted vector about the origin by $t$ radians. It has length $\sqrt 2$, and in its initial position it is already roated by $\pi/4$ radians. Thus, we can make the dotted vector by taking the sine, rotating it by an extra $\pi/4$ radians, and then scaling everything by $\sqrt 2$.
The generalization to $p\sin t+q\sin t$ should be clear.
Given $p \sin x + q \cos x$, divide the expression by $\sqrt{p^2+q^2}$ to get $a \sin x + b \cos x$ for $a^2 + b^2 = 1$. Now name $a = \cos \alpha$ and $b = \sin \alpha$. Notice that what you got is the expansion of $\sin(x+\alpha)$. In the given case, $a = b = \frac{\sqrt{2}}{2}$ so $\alpha = \frac{\pi}{4}$.
$$\sqrt 2\sin\left(x+\frac{\pi}{4}\right)=\sqrt 2\left(\sin x\cos \frac{\pi}{4}+\sin\frac{\pi}{4}\cos x\right)=$$ $$\sqrt 2\left(\sin x\frac{1}{\sqrt 2}+\cos x\frac{1}{\sqrt 2}\right)=\sin x+\cos x$$
$$\sin(x+y)=\sin(x)\cos(y)+\cos(x)\sin(y)$$
So to simplify your second expression write $p=r\cos(y)$ and $q=r\sin(y)$ so that $r=\sqrt{p^2+q^2}$ and $y=\arctan (\frac q p)$, then:
$$p\sin(x)+q\cos(x) = r\sin(x+y)$$
Proof without words
Remark for those who like:
$$ \frac{\sin \left(45^{\circ}+x\right)}{\sin x+\cos x}=\sin 45^{\circ}=\frac{1}{\sqrt{2}}\\ \Rightarrow \sin x+\cos x=\sqrt{2} \sin \left(45^{\circ}+x\right). $$
