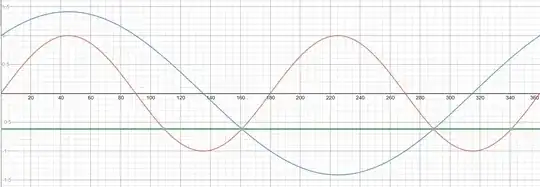
I am solving $\sin 2x = \sin x +\cos x $ for $0\le x \le 360$
$$\sin 2x = \sin x +\cos x$$ $$2 \sin x \cos x =\sin x + \cos x$$ $$(\cos x + \sin x) ^{2} - (\sin x)^{2} - (\cos x)^{2} =(\cos x + \sin x)^{2} - 1=\sin x + \cos x$$ Let $\cos x + \sin x = y$ $$y^{2} - 1= y$$ After solving the quadratic gets $1.618$(I think this is not accepted) and $-0.618$ $$y=\cos x + \sin x =\sin 2x = -0.618$$ $$2x=218.17,321.83,578.17,681.87$$ $$x=109.09,160.92,289.09,340.34$$ But the problem is $109.09$ and $340.34$ is not the solution. I didn't purposely square anything to produce extra solution. The two extra solution satisfy $\sin 2x=-0.618$ but not $\cos x + \sin x=-0.618$.Is there any mistake in my calculations, or is there anyplace I introduced accidentally extra solution? Thanks.