This is a very straight-forward question:
I'm trying to simplify $$\sin(2\pi t +\pi/4) + \sin(2\pi t -\pi/4)$$ and failing at it:
$\sin(2\pi t +\pi/4) + \sin(2\pi t -\pi/4)$
$2\sin(2\pi t)\cos(\pi/2)$ by sum $\to$ product = ZERO
Wolfram alpha gives $\sqrt{2}\sin(2\pi t)$, but gives no explanation as to how.
What am I doing wrong?
Hint: $$\sin(\alpha+\beta)=\sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta)$$
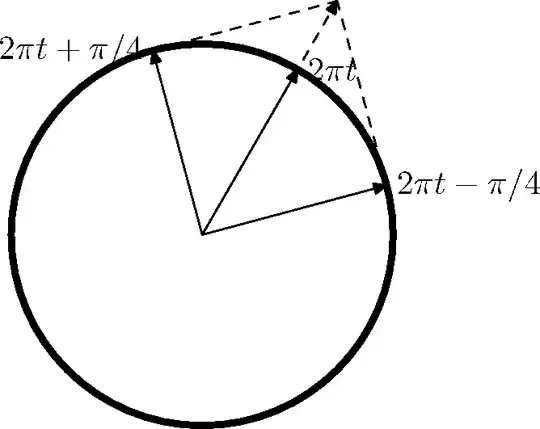
If you draw the situation on the unit circle, then $\sin\varphi$ is the x-coordinate of the point corresponding to the angle $\varphi$. The points $2\pi t-\pi/4$ and $2\pi t+\pi/4$ have right angle between them and $2\pi t$ is exactly in the middle.
So from the right triangle below you see that the sum of the vectors corresponding to $2\pi t-\pi/4$ and $2\pi t+\pi 4$ has the same direction as the vector corresponding to $2\pi t$ and the length is $\sqrt2$. The sum $\sin(2\pi t-\pi/4)+\sin(2\pi t+\pi/4)$ is the x-coordinate of this vector, and it is equal to $\sqrt2\sin 2\pi t.$
The same argument gives $\cos(2\pi t-\pi/4)+\cos(2\pi t+\pi/4)=\sqrt2\cos 2\pi t.$
More-or-less the same idea can be rewritten using complex numbers if we use Euler's forumula $e^{i\varphi}=\cos\varphi+i\sin\varphi$.
We have $$e^{\alpha+\pi/4}+e^{\alpha-\pi/4}=e^\alpha(e^{\pi/4}+e^{-\pi/4})=e^\alpha2\cos\frac\pi4=e^\alpha\sqrt2.$$ The real part gives $\cos(\alpha+\pi/4)+\cos(\alpha-\pi/4)=\sqrt2\cos\alpha$ and the imaginary part gives $\sin(\alpha+\pi/4)+\sin(\alpha-\pi/4)=\sqrt2\sin\alpha$.
Complex numbers are quite often useful for remembering/proving trigonometric identities.
If you want to use the sum-product formula, it should be the right one. We have $$\sin x+\sin y=2\sin\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2}\right).$$ But I think it is better to go back to the addition/subtraction laws for sine, as described by Zev Chonoles.
We have $$\sin(a+b)=\sin a\cos b+\cos a\sin b,$$ and its very close relative $$\sin(a-b)=\sin a \cos b -\cos a\sin b.$$ Let $a=2\pi t$ and $b=\frac{\pi}{4}$. The sine and cosine of $\frac{\pi}{4}$ are both $\frac{1}{\sqrt{2}}$.
Remark: If one will be doing a certain type of calculation very often, it is useful to commit to memory any relevant formulas. However, it is I think best to know only a quite small number of trigonometric facts, and reconstruct anything else one may need.
