What are the best examples of mathematical induction available at the secondary-school level---totally elementary---that do not involve expressions of the form $\bullet+\cdots\cdots\cdots+\bullet$ where the number of terms depends on $n$ and you're doing induction on $n$?
Postscript three years later: I see that I phrased this last part in a somewhat clunky way. I'll leave it there but rephrase it here:
--- that are not instances of induction on the number of terms in a sum?
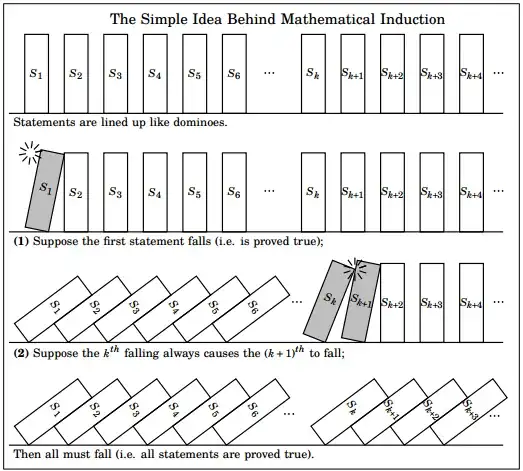
Here is the first example I saw of induction, and I still think it's a beautiful one.
Problem: Prove that a $2^n \times 2^n$ sheet of graph paper with one box removed, can be tiled with L-shaped trominos.
Proof: For the $n=1$ case, there is nothing to prove: a $2 \times 2$ grid with one box removed is exactly a L-tromino.
For $n=2$, consider the $4 \times 4$ grid. You can divide it into four $2\times 2$ grids. The removed box is in one of those four sub-grids, so that sub-grid can be covered with an L-tromino (is an L-tromino, rather). What about the other 3 sub-grids? Put an L-tromino right in the center of the huge grid, which covers them!
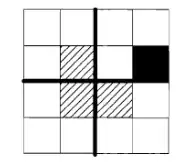
Now the remaining part of each of them is a $2\times2$ grid with one box removed. I leave it to you to complete the proof, and teach it to the students as you best see fit.
The figures above are from Mathematical Circles: Russian Experience by Dmitri Fomin, Sergey Genkin, and Ilia Itenberg, specifically the chapter on Induction which is written by I.S. Rubanov. The book actually doesn't use a variable $n$, but asks for a $16\times 16$ square, then in the form of a discussion between a teacher and a student works through the $2\times 2$ and $4\times 4$ and $8\times 8$ cases, until it is obvious that we have in fact proved a theorem for any $2^n \times 2^n$ ('It looks like we have a "wave of proofs running along the chain of theorems $2\times2 \longrightarrow 4\times4 \longrightarrow 8\times8 \longrightarrow$ It is quite evident that the wave will not miss any statement in this chain.')
As an aside, this is a lovely book with quite a bit of non-trivial mathematics suitable for elementary school and high-school students (though I read in late high school).
This theorem and proof are also on the cut-the-knot website: Tromino Puzzle and Golomb's Inductive Proof.
My favorite induction problem goes like this:
Consider a long circular road that has a number of fuel depots along the way. All in all, the depots contains just the right amount of fuel to get your car around. You start with an empty tank. Show that you can always find a depot at which to start so that it's possible to get all the way round. (You can make the road one-way if you like.)
Some I can think of off the top of my head:
Number of moves to solve the Towers of Hanoi puzzle.
Factorization into primes (uses strong induction, though).
Also using strong induction, the winning strategy for a simplified game of nim described at the bottom of this answer.
Formula for combinations, using $\binom{n+1}{k} = \binom{n}{k}+\binom{n}{k-1}$.
I'll add more later if I think of any.
All sorts of stuff about the Fibonacci numbers.
a. Many, many identities such as $F_n^2 = F_{2n}\pm1$.
b. The number of domino tilings of a $2\times n$ rectangle.
c. The closed-form formula for Fibonacci numbers in terms of $\frac12(1+\sqrt5)$.
Analogously, all sorts of stuff about recursively-defined anything.
a. For example, let $a_0 = 2$, and $a_{i+1} = 3a_i +2$; show that $a_i = 3^i-1$. It's easy to make up such identities.
b. As Brian Scott suggested, stuff about binary trees. Lots of combinatorial identities: How many full binary trees are there of order $n$? How many paths from the upper right corner of an $n\times n$ checkerboard to the lower left? How many ways to lace a sneaker with $n$ pairs of holes?
c. High school students love higher dimensional geometry. Count the number of vertices, edges, etc. in an $n$-cube.
d. There is an infinite family of solutions to $|a^2 - 2b^2| = 1$, because $(1,0)$ is a solution, and if $(a_i, b_i)$ is a solution, then so is $(a_i + 2b_i , a_i + b_i) $.
e. Or you can present the preceding in terms of "Let's find rational approximations to $\sqrt 2$". Make a table of $n^2$ and another table of $2n^2$. Find entries in the left table that are close to entries in the right table. This gives approximations $\frac11, \frac32, \frac75, \frac{17}{12}, \frac{41}{29}\ldots$. Guess that the next term is $a_i+2b_i\over a_i+b_i $ and prove by induction that with this definition, $(a_n,b_n)$ satisfies the equation and that $a_n\over b_n$ is close to $\sqrt2$.
f. Consecutive elements $\frac ab, \frac cd$ of the Farey series always satisfy $bc-ad = 1$. Other stuff related to the Stern-Brocot tree.
Let $a_i = \langle 4, 484, 48484, \ldots\rangle$ and $b_i = \langle 8, 848, 84848, \ldots\rangle$.
a. Show that for each $i$, $4b_i - 7a_i = 4$
b. Let $c_i$ be the concatenation of $a_i$ and $b_i$, so for example $c_2 = 484848$. Then $c_i = b_i^2 - a_i^2$.
I'd use a visual method to explain the concept before "complicating" it with numbers. Falling dominoes seem intuitive and capture the essence of induction.
To visualize it, think of the statements as dominoes, lined up in a row. Imagine you can prove the first statement S1, and symbolize this as domino S1 being knocked down. Additionally, imagine that you can prove that any statement Sk being true (falling) forces the next statement Sk+1 to be true (to fall). Then S1 falls, and knocks down S2. Next S2 falls and knocks down S3, then S3 knocks down S4, and so on. The inescapable conclusion is that all the statements are knocked down (proved true).
(Source: p143 of Book of Proof by Richard Hammack)
(You could also go off on a tangent about abstraction in mathematics analogies.)
Real dominoes and the algorithmic explanation was my attempt at a joke. Ha. Although, a good physical analogy can be a powerful visualising tool - e.g. domino computer https://www.youtube.com/watch?v=OpLU__bhu2w
People learn in a variety of styles, so perhaps mix up the delivery method a bit if they still don't get it.
– aportr Jan 27 '15 at 14:34I like the ones that involve division.
For instance, prove that $7 \mid 11^n-4^n$ for $n=1, 2, 3, \cdots$
Another example would be perhaps proving that
$$(3+\sqrt{5})^n+(3-\sqrt{5})^n$$
is an even integer for all natural numbers $n$.
Does proving statements like $f(n) \leq g(n)$ fit your bill? For instance, prove that $2^n \leq 2n!$.
These come to mind immediately; I may have more later.
The number of vertices in a tree is one more than the number of edges.
If $n>0$, exactly half of the subsets of $\{1,\dots,n\}$ have even cardinality.
Any of the many two implies finite arguments. For example, if $\mathscr{C}$ is a collection of sets with the property that $C_0\cap C_1\in\mathscr{C}$ whenever $C_0,C_1\in\mathscr{C}$, then $\mathscr{C}$ is closed under finite intersections.
The postage stamp induction: given an unlimited supply of $3$ and $5$ cent stamps, every integer amount greater than $8$ can be made. Or if you prefer: if $A$ is a set of positive integers such that $3,5\in A$ and $a+b\in A$ whenever $a,b\in A$, then $A$ contains every integer greater than $8$.
All sorts of simple inductions based on recursive definitions of strings of symbols. For example, $aba$ is a legal word, and if $w$ is a legal word, so are $abw,awb,wab,baw,bwa$, and $wba$; prove that every legal word contains more $a$’s than $b$’s.
How about that a graph always has an even number of vertices of odd degree, by induction on the number of edges? But perhaps the counting argument is simpler.
Along the same lines: Euler's $F-E+V=2$ formula for graphs. Chromatic polynomials.
The number of diagonals in a convex polygon is $n(n-3)/2$.
Proof
For $n=3$, the result follows.
Suppose true for $n$ and look at $n+1$. By joining vertex $1$ with vertex $3$, we obtain a polygon with $n$ sides. The inductive hypothesis means we have $n(n-3)/2$. diagonals, plus the one we just drew. We only need to add the missing diagonals from $2$ to all other vertices $\neq 1,3$, which accounts to $n-2$ more diagonals. Thus we get $$\frac{n(n-3)}2+n-2+1=\frac{n(n-3)+2(n-1)}{2}=\frac{n^2-n-2}{2}=\frac{(n-2)(n+1)}2$$
and the result follows.
Check this http://www.youtube.com/watch?v=oU60TuGHxe0&t=3m9s. Mathematical induction explained on simple properties of strings.
I think we did things we already knew to start with, like the formula for triangular numbers, then squares. The binomial coefficients provided examples too. Actually this developed into expressions for the coefficients of power series and generating functions.
There is some magic in discovering such things for yourself rather than being told. My maths teacher pointed me in the right direction and let me discover ...
Sometimes no-examples teach a good deal. Check the following proof that all human beings on Earth right now are the same age:
Proof for 1: clearly, in a set with only 1 person all the people in it are the same age
Inductive hypothesis: in all the sets with n persons we have that all of them are the same age.
Let A be a set with $n+1$ persons, say $A=\{a_1,...,a_n,a_{n+1}\}$, and let $A':=\{a_1,...,a_n\}$ , $A'':=\{a_2,...,a_{n+1}\}$ . The ind. hyp. tells us that all the persons in A' are the same age and all the persons in A'' are the same age, and since $a_2$ belongs to both then all the elements in A are the same age as $a_2$ , ergo: all of the elements in A are the same age. QED.
At the risk of beating a dead horse, any good book on competition mathematics is sure to have lots of examples at the level you want. Here's one from Putnam and Beyond by Gelca and Andreescu, which demonstrates how recursive definitions can be used to do induction:
Prove that any function $f : \mathbb{R} \rightarrow \mathbb{R}$ can be written as a sum of two functions, each of which is a shift of an odd function (i.e. there exists some $g,h : \mathbb{R} \rightarrow \mathbb{R}$ and $a,b \in \mathbb{R}$ such that $g(x-a)$ and $h(x-b)$ are odd functions and $f = g+h$)
The proof is by constructing $g$ and $h$ on increasing subintervals of $\mathbb{R}$, with $a=0$ and $b=1$. Let $g(x)=x f(1)$ on $[-1,1]$, and $h(x)=f(x)-g(x)$ on the same interval. For $n \ge 1$ let $h(x)= -h(2-x)$ on $(2n-1,2n+1)$ and $g(x)=f(x)-h(x)$ on the same interval. Then let $g(x)=-g(-x)$ on $[-2n-1,-2n+1)$ and $h(x)=f(x)-g(x)$ on the same interval.
To prove that $g$ and $h$ defined this way satisfy the required properties uses induction. Specifically, assume at each stage, we have $g$ and $h$ defined on $[-2n-1,2n+1]$ with $f=g+h$, $g$ odd, and $h(x)=-h(2-x)$ for $x \in [-2n-3,2n+1]$. It follows directly from the definitions of $g$ and $h$ that $f=g+h$ on $[-2(n+1)-1,2(n+1)+1]$ and that $g$ remains odd and $h(x)=-h(2-x)$ for $x \in [-2(n+1)-3,2n+1]$. Since these intervals cover $\mathbb{R}$ we have $g$ and $h$ defined everywhere with the desired properties.
Admittedly, this is a bit harder than what most secondary students would be able to solve, but it is still totally elementary and with some watering down and drawing pictures they could at least understand it.
Why not some properties of powers of (natural) numbers: $$\forall\,a,b,m,n\in\mathbb{N}\setminus\{0\},\quad a^m\cdot a^n=a^{m+n},\quad (a^m)^n=a^{mn},\quad a^n\cdot b^n=(ab)^n.$$
Another one, which is not totally elementary as you meant it but I think may be very formative in secondary school level is the following:
If $p$ is a polynomial in variable $x$, its degree is $\deg(p)=n\ge 1$, its coefficients $a_0,\ldots,a_n\in\mathbb{R}$, then for all $x_0\in\mathbb{R}$, exist $b_0,\ldots,b_n\in\mathbb{R}$ such that $$p(x)=\sum^n_{k=0}b_k(x-x_0)^k,\quad\forall\,x\in\mathbb{R}.$$
This can be shown very quickly also without induction and has a nice meaning in the $x,y$ plane drawn on the blackboard.
For any given number of colors c, and any given integers n1, . . . ,nc, there is a number, R(n1, ..., nc), such that if the edges of a complete graph of order R(n1, . . . , nc) are colored with c different colors, then for some i between 1 and c, it must contain a complete subgraph of order ni whose edges are all color i.
The two color case should be introduced first, of course. If the children get a good feel for this case, then they can attempt to understand the proof for this special case and then later move on to understand the general theorem and the proof of that.
Suppose that in a group of $2n + 1$ people, for every group of $n$ people there exists one person (which is not one of them) who knows each of them. Here the relation "knows" is symmetric.
Then, there exists one person who knows all the other $2n$ people.
Maybe it would be good to start with something that the students already know is obviously true. For example, you could develop an inductive proof that $2n$ is always even.
I think this would make it easy for them to see what the base case, inductive hypothesis and inductive steps mean.
For the base case we show our statements holds for the smallest possible $n$. In this case it is $0$ and $2(0)=0$, which is even.
For the inductive step we have to show that $2(n+1)$ is even but we get to use the inductive hypothesis: $2n$ is even. Then it's just a matter of the distributive property to get $2n+2$ and the common knowledge that adding $2$ to an even number gets another even number.
Other candidates could be anything shown with straightforward structural induction on Peano numbers.
