Proof that given 8x8 Mboard and 21 trominoes there will no overlap

Question

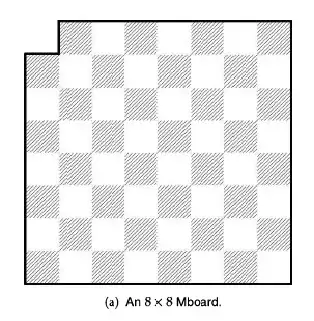
Given an 8x8 Mboard ( top left piece missing), as given below in the image, and 21 trominoes, how can we proof that there exists a configuration where there will be no overlap after all trominoes are placed.

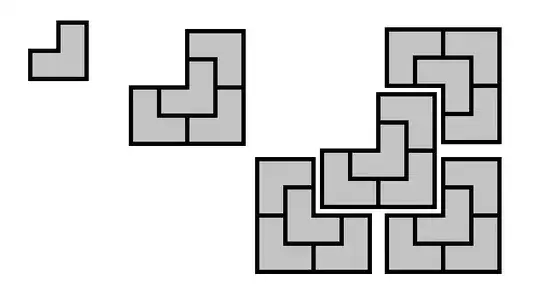
What I tried doing was - a 8x8 Mboard will have 63 squares, now $63 / 21 = 3$, ie. it is divisble. But recall a tromino is L-shaped, so just show that the total number of squares is divisble with the total number of trominoes really isnt telling much. I mean how do you account for the shape of the tromino in that case.

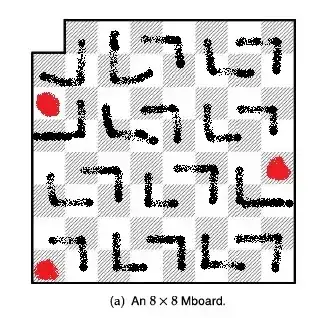
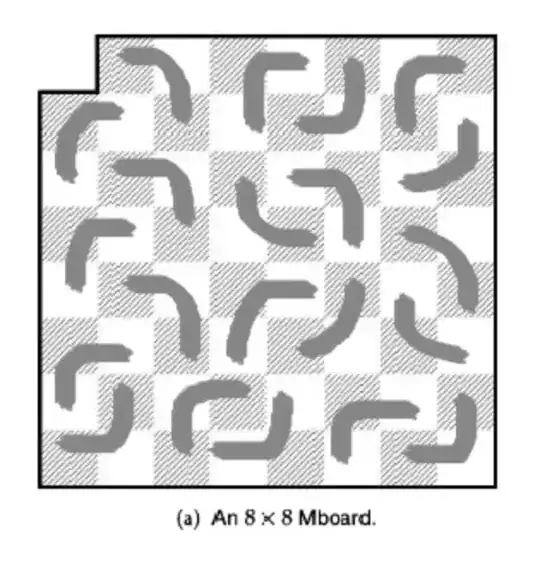
I actually manually plotted out a configuration but could only get up 20 trominoes to fit. I have no idea how 21 fits in, and how we can say that there will be no overlap.

The red squares are the squares that were blank. There are 3 of them, but how can we rearrange the configuration to included 21 trominoes. And more than that how can we say that there will be no overlap?

If you use 20 trominoes, you should have $(8 \cdot 8 - 1) - (20 \cdot 3) = 63 - 60 = 3$ red tiles. Indeed, in your second figure, the bottom left square should be colored red. — parsiad, Jul 18 '19 at 08:08
Also, apart from the tromino completing the top left 2x2 corner, you can easily fill in the rest of the board with 2x3 blocks. Then you can split all the 2x3s into two trominoes. — Jyrki Lahtonen, Jul 18 '19 at 08:31
Fun fact: There are exactly 30355 ways to tile the chessboard with one corner missing. 15178 solutions if we consider mirror images as the same solution. This means that there's only one solution that has mirror symmetry! — John Dvorak, Jul 18 '19 at 08:32
@ng.newbie Presumably by just doing it. Tell a computer to try every way, and have it count them. It's possible that there is some other, really clever way to do it, but I doubt it. It seems like a mess to count by hand. — Arthur, Jul 18 '19 at 08:38
@ng.newbie look up "burr tools" (freeware). Really fast in this instance, too. — John Dvorak, Jul 18 '19 at 08:54

Arthur · Answer 1 · 2019-07-18T08:28:31.123

6

Instead of filling in row-by-row, go layer-by-layer. First tackle the $2\times 2$ with one corner missing. This is trivial. Now tackle the $4\times 4$, by first covering the top $2\times 2$ the way you did.

Here is the kicker: The way you placed your trominoes in this last step makes them one large tromino! (They cover the $4\times4$ board except the top $2\times2$.) Now you can tackle the $8\times8$ by first taking the top $2\times2$, then the top $4\times4$, then take the rest of the board using your large tromino piece. This makes this last step identical to the $4\times 4$ covering, only scaled up.

edited Jul 18 '19 at 08:28

answered Jul 18 '19 at 08:19

Arthur

199,419

tell me given the total number of squares and the number trominoes, is it possible to tell whether there will be any overlap or not ? If so how is that possible ? I guess thats what I am really asking. – ng.newbie Jul 18 '19 at 08:20
So Arthur proves that the task is possible irrespective of which of the 64 squares is missing. This is a classic puzzle. We may have covered it earlier. IIRC I've seen the 3D version with a $2^n\times 2^n\times 2^n$ cube with a single $1\times1\times1$ prefilled to be filled it with blocks of $2\times2\times2$ minus one corner. But +1 anyway. – Jyrki Lahtonen Jul 18 '19 at 08:24
2

@ng.newbie Yes, it's possible to tell. If it's possible, then a proof will consist of giving an example of it being done. If it's impossible, then a proof will consist of some reason it just can't be done. For instance, it's impossible by using $20$ trominoes, because the number of squares doesn't match up. It's impossible using any number of dominoes because the board has an odd number of squares. That kind of argument will show impossibility. But there is no good, general way to show that it is possible except just doing it. – Arthur Jul 18 '19 at 08:25
Not surprisingly this has been done at least twice before. In addition to my suggested duplicate target see also here. – Jyrki Lahtonen Jul 18 '19 at 08:28
Oh, you had a slightly different recursion in mind. Sorry about jumping the gun a bit. Many ways to do this. – Jyrki Lahtonen Jul 18 '19 at 08:32
@JyrkiLahtonen I read in a comment somewhere recently that there are over 30000 ways. – Arthur Jul 18 '19 at 08:34

parsiad · Answer 2 · 2019-07-18T08:16:27.753

3

edited Jul 18 '19 at 08:16

answered Jul 18 '19 at 08:14

parsiad

25,154

@parisad Any intution for this? because I can't undertsand why this works. Any mathematical proof for this exists ? – ng.newbie Jul 18 '19 at 08:16
This is a mathematical proof. As for intuition, you could try breaking up the board into smaller chunks and cover each chunk separately. – parsiad Jul 18 '19 at 08:17
@parisad Ok just tell me given the total number of squares and the number trominoes, is it possible to tell whether there will be any overlap or not ? If so how is that possible ? I guess thats what I am really asking. – ng.newbie Jul 18 '19 at 08:19
See @Arthur's answer. – parsiad Jul 18 '19 at 08:21
@parisad Also could you help me out and tell me which branch of mathematics this falls under. Is it a tiling problem? If so I will study them to gain more insight. – ng.newbie Jul 18 '19 at 08:21

score 3 · Answer 3 · answered Jul 18 '19 at 08:27

3

This picture shows how you can build up the solution, exactly as Arthur describes in his answer.

answered Jul 18 '19 at 08:27

Jaap Scherphuis

13,660

Proof that given 8x8 Mboard and 21 trominoes there will no overlap

3 Answers3