Is there any way that one can describe all the roots of the incomplete gamma function $\Gamma(n,z)$, for $n\in \mathbb{N}$, analytically?
2 Answers
(This was supposed to be another comment to Raymond's answer, but it got too long.)
As already mentioned by Raymond, we have the relationship (using slightly different notation)
$$\Gamma(n,z)= (n-1)! \exp(-z) e_{n-1}(z)$$
where
$$e_n(z)=\sum_{k=0}^n \frac{z^k}{k!}$$
the partial sums of the Maclaurin series for $\exp(z)$, is sometimes called the exponential sum function. Though a general closed form for the roots of $e_n(z)$ is not known, the distribution of the roots of the polynomial $e_n(nz)$ in the complex plane is pretty well studied:
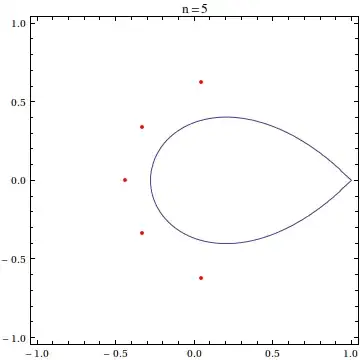
In particular, Gábor Szegő (1924) and Jean Dieudonné (1935) both showed that the roots of the scaled exponential sum function $e_n(nz)$ approach the portion of the curve $|z\exp(1-z)|=1$ (now often referred to as the Szegő curve) within the unit disk as $n\to\infty$. In two papers, Carpenter, Varga, and Waldvogel study the asymptotics of the zeros of $e_n(nz)$. Other papers of interest include those by Buckholtz, Newman and Rivlin (with correction), Conrey and Ghosh, Pritsker and Varga, Walker, and Zemyan. (These are the ones I've read; I'm sure there are other nice papers I've missed.)
- 75,051
-
4Thanks for the interesting links and nice illustration! I'll just add that the second paper of Varga and Carpenter 'Asymptotics for the zeros of the partial sums of e^z. II' (and many others on the same subject and the related 'partial sums of $\cos(z)\ $ and $\sin(z)\ $') are available at Varga's homepage. Cheers, – Raymond Manzoni Feb 15 '12 at 20:11
-
Very nice, Thanks so much for the graph and references. – K1. Feb 16 '12 at 02:00
-
This may also be interesting. – Jean-Claude Arbaut Nov 05 '15 at 13:44
With the usual definition we have : $$\Gamma(n,x)=\int_x^{\infty} t^{n-1} e^{-t} dt$$
After repeatedly using integration by parts we may get this formula : $$\Gamma(n,x)= (n-1)! e^{-x} \sum_{k=0}^{n-1} \frac{x^k}{k!}$$ so that you are asking for the zeros of the polynomials : $$P_n(x)=\sum_{k=0}^{n-1} \frac{x^k}{k!}$$ Let's search the first solutions :
$ \begin{array} {rcc} n & P_n(x) & \mathrm{zeros} \\ \hline \\ 1 & 1 & \emptyset \\ 2 & 1+x & \{-1\} \\ 3 & 1+x+\frac{x^2}{2!} & \{-1-i,-1+i\} \\ 4 & 1+x+\frac{x^2}{2!}+\frac{x^3}{3!} & \{\sqrt[3]{\sqrt{2}-1}-\frac1{\sqrt[3]{\sqrt{2}-1}}-1,..,.. \} \\ \end{array} $
I'll stop here because the algebraic expressions of the zeros are becoming rather long and complicated... (search others with WolframAlpha)
Or did you hope something simpler?
- 43,021
- 5
- 86
- 140
-
3MathWorld refers to these polynomials as exponential sum functions, $e_n(x)$. – J. M. ain't a mathematician Feb 15 '12 at 01:21
-