1

I'm trying to experiment with zeros of the $e^{z^2}$ function ( also $ ch(z)$ and $\xi(1/2+z)$) For $e^{z^2}$ Taylor series about $z=0$, we have:

$$ e^{z^2}=\sum_{m=0}^{\infty} \frac {z^{2m}}{m!}$$

Below are the pictures of location of zeros on the complex plane for four partial sums $S_{2M}=\sum_{m=0}^{2M} \frac {z^{2m}}{m!}$ for $2M=38, 50, 54, 74$:

My question: Is the observed complex behavior — splitting in the region of the complex axis an artifact (possible errors in calculating the roots, i.e., flaws in numerical calculations) or is this the real behavior of zeros with increasing $M$?

Aleksey Druggist
  • 416
  • See Roots of the incomplete gamma function and the links in the "Linked" list in the right bar. That there is a square root in translating the results is a trivial difference. – Lutz Lehmann Oct 21 '19 at 13:52
  • The square root of the mentioned Szegő curve looks more like your first plot, the splitting of the curve in the last plots is more likely an artefact of numerically finding roots in finite-precision floating-point, see the Wilkinson test polynomial for a demonstration of this effect in a more controlled situation. – Lutz Lehmann Oct 21 '19 at 14:25
  • An elementary derivation of the equation for the Szegő curve can be found in Complex zeros of the polynomials $\sum_{k=0}^{n} z^k/k!$, inside balls. – Lutz Lehmann Oct 21 '19 at 17:31
  • @LutzL, thanks a lot, I would like to first of all to understand the reason for the failure in numerical methods. You mentioned Wilkinson test polynomial. Could you explain the main idea qualitatively, I have not yet found a link that would clarify the situation for me – Aleksey Druggist Oct 21 '19 at 18:04
  • 1
    Rounding while converting the coefficients to floating point constitutes a perturbation. For single, well isolated roots, this only results in a perturbation of the same size in the root value. A cluster of $m$ roots behaves more like a root of multiplicity $m$, a perturbation of size $\mu$ in the coefficients then leads to a perturbation of size $\mu^{1/m}$ in the roots, usually exploding the roots away from the center of the cluster. This root perturbation can easily reach visible distortions in the root plot. – Lutz Lehmann Oct 21 '19 at 20:44
  • 1
    If you multiply the $2M=40$ case with $40!$ so that all coefficients are integer, you get a different error picture in the roots plot. Esp. the web tool finds $\pm 0.5$ as roots, which is obviously wrong. // However, giving the partial exponential sum directly as is, with rational coefficients, returns a perfectly looking root plot. – Lutz Lehmann Oct 21 '19 at 21:17

1 Answers1

1

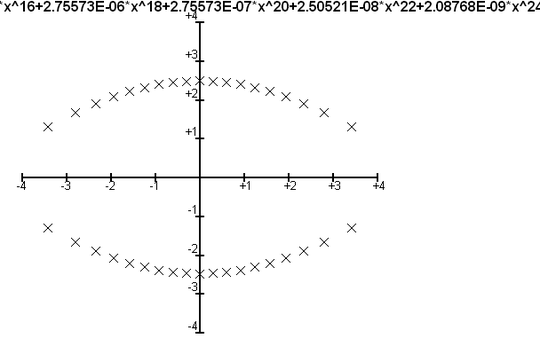
Using a CAS like Magma, one can construct the partial sums in one line.

PS<x>:=PowerSeriesRing(Rationals());
Truncate( Exp(x^2+O(x^81)) );

Inserting this into the cited web tool results in the root graph

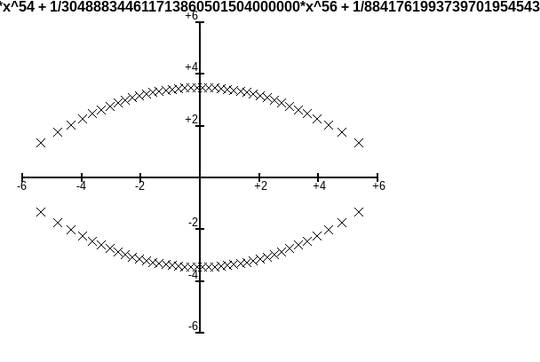
enter image description here

This is what one expects from the square root of the Szegő curve $|ze^{1-z}|=1$ inside the disk $|z|<1$, see derivation and visualization. The roots of $s_n(nz)$, where $s_n$ is the partial exponential sum, converge towards this curve, and thus the roots of the given polynomials $s_{2M}(z^2)$ towards its square root, scaled by $\sqrt{2M}$.

How did the split of the curve happen? Depending on how the web tool reads its input, there could be errors in reading integers or some other strange happening, as making the coefficients integer via

Truncate( Factorial(40)*Exp(x^2+O(x^81)) );

results in a root plot

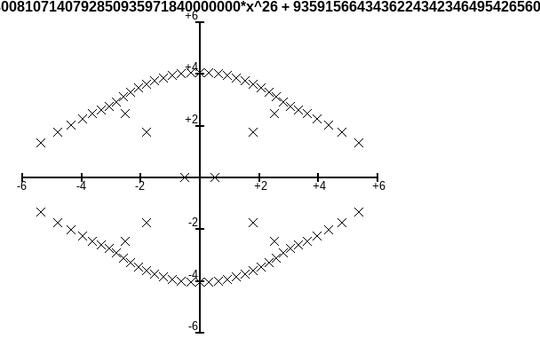
enter image description here

It is unclear how $x=\pm 0.5$ could be detected as roots, as all coefficients are positive.

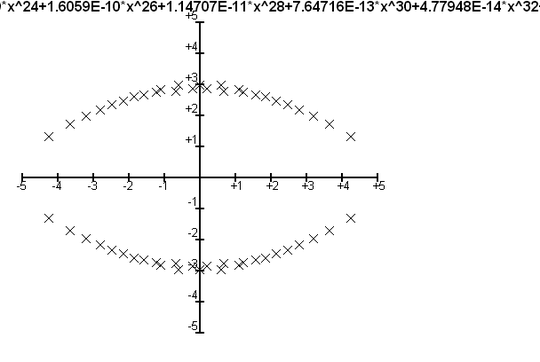
To get a pattern similar to the one you observed, I have to reduce the relative accuracy of the floating-point coefficients to 8 digits

PS<x>:=PowerSeriesRing(RealField(8)); 
Truncate( Exp(x^2+O(x^(81))) );

to get then a slightly larger split

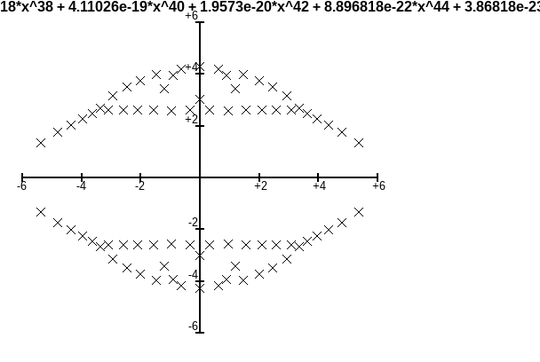
enter image description here

While the root set is continuous as set under changes of the polynomial coefficients, multiple roots or patterns close to that, that is, root cluster, will change especially rapidly. While there are directions that move a cluster towards joining roots, these are sparse. Random changes in the coefficients will expand the cluster, as observed in this graph.

Lutz Lehmann
  • 126,666
  • Thank you so much! You not only gave a very qualified answer, but also allowed me to solve my problem. I set the parameter to 2M = 100, the result - no splitting! I believe the same situation will be for series of ch(z) and $\xi(1/2+z)$ – Aleksey Druggist Oct 22 '19 at 09:21