Given $f(z)$ holomorphic in some $\Omega$ (feel free to take any condition you want on $\Omega$), what is the relationship between the root of $f(z)$ and the roots of the truncated expansion of $f(z)$?
Let
$$
f(z) = \sum_{k=0}^{\infty} a_k z^k
$$
and define
$$
p_n(z) = \sum_{k=0}^{n} a_k z^k.
$$
If $f$ has a zero $z_0$ of multiplicity $m$ then Hurwitz's theorem tells us that $p_n$ has precisely $m$ zeros near $z_0$ for large enough $n$, and that these $m$ zeros converge to $z_0$ as $n \to \infty$.
Of course, a not-identically-zero analytic function can only have finitely-many zeros in any compact subset of its domain, so these extra zeros of $p_n$ as $n \to \infty$ must essentially be leaving the domain of $f$.
If $f$ is not entire, then it is a classical result of Jentzsch${}^1$ that each point on the circle of convergence of the power series is a limit point of the zeros of the partial sums $p_n$.
In 1922, Szegő${}^2$ sharpened Jentzsch's result as follows:
Jentzsch-Szegő Theorem.
Let $\Lambda \subset \mathbb N$ be a subsequence such that
$$
\lim_{k \in \Lambda} |a_k|^{1/k} = 1/R > 0.
$$
If we denote the number of zeros of $p_n$ in $U \subset \mathbb C$ by $Z_n(U)$, then
$$
\lim_{n \in \Lambda} \frac{Z_n(\{z : |z| < r\})}{n} = 1 \quad \text{and} \quad \lim_{n \in \Lambda} \frac{Z_n(\{z : a < \arg z < b\})}{n} = \frac{b-a}{2\pi}
$$
for any $r > R$ and $0 < b-a < 2\pi$.
This basically says that the zero counting measures of the partial sums $p_n$ converge in the vague topology to the uniform distribution on the circle of convergence of the power series. A modern treatment of this and related results can be found in the book Discrepancy of Signed Measures and Polynomial Approximation by Andrievskii and Blatt.
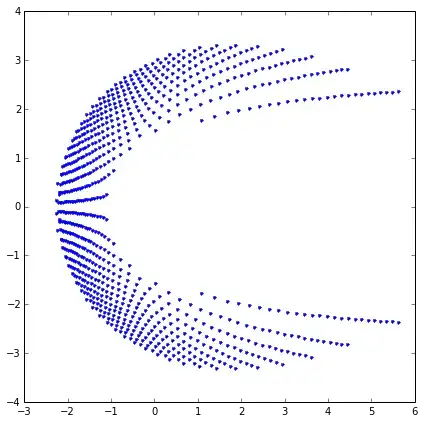
If $f$ is entire then the behavior of the zeros of the partial sums is very different, as the example with $f(z) = e^z$ illustrates. In order to leave the domain of $f$, the zeros of $p_n$ which don't converge to zeros of $f$ must tend to $\infty$. How quickly they travel, and with what distribution, is a complicated question.
In his PhD thesis, Rosenbloom${}^3$ showed that these "extraneous" zeros of $p_n$ generally grow at a rate comparable to $|a_n|^{-1/n}$ as $n \to \infty$, and gave a general formula for their limit curves (after an appropriate scaling). A statement of his main result is given on p. 6 of my master's thesis.
There are still many problems to explore. For example, can we quantify how quickly the scaled zeros approach their limit curve? So far this has been done in some particular cases, but little has been done in general.
1. Robert Jentzsch, Untersuchungen zur Theorie der Folgen analytischer Funktionen. (German) Acta Math. 41 (1916), no. 1, 219–251.
2. Gabor Szegő, Über die Nullstellen von Polynomen, die in einem Kreis gleichmässig konvergieren, Sitzungsber. Ber. Math. Ges. 21 (1922), 59–64.
3. Paul Charles Rosenbloom, On sequences of polynomials, especially sections of power series, Ph.D. thesis, Stanford University, 1944, Abstracts in Bull. Amer. Math. Soc. 48 (1942), 839; 49 (1943), 689.