2

Good day. I am interested in an IMPLEMENTED, not theoretical, example of code for solving the problem of finding the INDEX of an element in an uncorrected array using Grover's Algorithm. The task looks like this: there is an array [3,6,2,4,9,0,1,5] and it is necessary to determine the index of the element in this array, which is 9 (that is, the result should be 4). I fully understand the example of Grover's algorithm implementation here from qiskit https://qiskit.org/textbook/ch-algorithms/grover.html, but I cannot transform it to solve the real problem described above. It is desirable to present the solutions on qiskit in Python. P.S. I have seen these links, but this all does not provide clarity for me and understanding of how to implement this task: 1, 2, 3, 4. I would be very grateful for a detailed explanation.!

After first answer I have questions described in comments and this image : question

original image link

glS
  • 24,708
  • 5
  • 34
  • 108
Sergey Ivanow
  • 31
  • 4
  • Could you please explain where is quantum computing used in this case? – Maf Mar 28 '21 at 12:13
  • @Maf I'm just starting to study this question, so I can't give you a qualified answer – Sergey Ivanow Mar 30 '21 at 19:30
  • Hi, I am currently working on same problem of a simple database search (like a text file with some entries) using Grover and came across your question. Do you have the source code with which you were able to solve this search prob? – aneela Jul 28 '22 at 06:51

1 Answers1

4

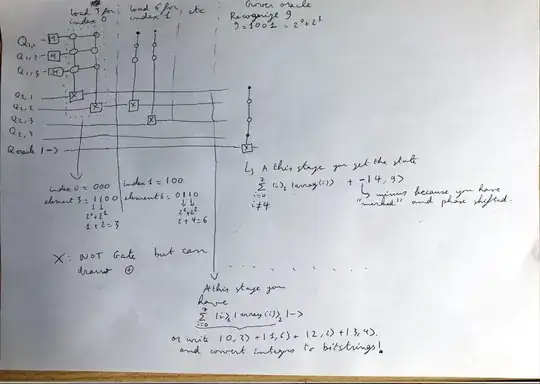
In your case, the array would have to be inputed into the quantum circuit. Usually in Grover, this is let to the oracle who would have some access to it, or to a Quantum Random Access Memory (or QRAM) that would load it for you efficiently (but unfortunately it is not there yet).

What you would need in your case is 3 qubits for encoding indices (as you have an array of length 8 -- let's call them register 1) and you would need an extra 4 qubits (where you can have as bitstrings all integers between 0 and 16, as your maximum is 9 -- let's call them register 2). Also probably extra qubits for other operations like phase shift and your oracle.

So we can write as: $ | 0 \rangle_1 | 0 \rangle_2 | 0 \rangle_{extra} $. Applying Hadamard transform on register 1 will then give you: $ \sum_{i=0}^{7} | i \rangle_1 | 0 \rangle_2 | 0 \rangle_{extra} $

Of course, you want first an operator to load your array (assuming no code does it for you at the moment). You want to end up with the state: $$ \sum_{i=0}^{7} | i \rangle_1 | array(i) \rangle_2 | 0 \rangle_{extra} $$ where $array(i)$ corresponds to the $i$-th element.

Unefficiently, you have to loop over each index (represented by a bitstring in register 1) and apply a control operation that will load $array(i)$ represented by a bitstring in register 2. So a sequence of multi-controlled NOTs for bitstring loading. As an example, say you want to load the third element which is $2$ (and its index in the array is 2) and in bitstring $010$ with $3$ qubits or $0100$ with $4$ (or $0010$ in reverse order depending how you read). So your multi-control check in register 1 that the index is $010$ and apply a NOT gate such that the value in register 2 corresponds to element $2$ (the NOT will be on the second qubit of register 2 -- or the third in reverse order).

Finally, in your case you need to implement for Grover iterations, the operation that identify the element $9$. This is again a multi-controlled NOT where you control on register $2$ that the bitstring you look at is $9$ ($1001$) and the NOT will be on the phase shift qubit for Grover to mark that state.

Then with these operations, you do your Grover iterations as usual. I won't have code to show but figuring this out is a good exercise.

EDIT: Sorry I draw and write really bad... Drawing asked explaining a few steps

cnada
  • 4,754
  • 1
  • 8
  • 21
  • Thanks! This part is not completely clear to me: "So your multi-control check in register 1 that the index is 010 and apply a NOT gate such that the value in register 2 corresponds to element 2 (the NOT will be on the second qubit of register 2 -- or the third in reverse order). Finally, in your case you need to implement for Grover iterations, the operation that identify the element 9. This is again a multi-controlled NOT where you control on register 2 that the bitstring you look at is 9 (1001) and the NOT will be on the phase shift qubit for Grover to mark that state." – Sergey Ivanow Mar 25 '21 at 19:10
  • I realized that I need to start 2 quantum registers. In one case, I will feed the Grover algorithm the values of the indices of the elements (or rather their super position, since I apply the Hadamard operator to all of them), and in the second case, I must also write the superposition of all the numbers from 0 to 16 (i.e. Also apply the Hadamard operator for all four qubits of the second register)? Need separate oracles for both checking case 1 and checking case 2? Or only for register 2? – Sergey Ivanow Mar 25 '21 at 19:11
  • And if there should be oracles for both registers, what should each of them check and what should happen after each of them checks? – Sergey Ivanow Mar 25 '21 at 19:11
  • See to image in edited question please. – Sergey Ivanow Mar 25 '21 at 19:37
  • 1
    +1. cnada is back! – user1271772 No more free time Mar 25 '21 at 19:40
  • @SergeyIvanow No you should not apply a Hadamard transform to the second register. But your first "oracle", or should I say operator, would load elements for having with the superposition of indices (register 1) their corresponding elements in register 2. So you can think of register 2 as a working register you will work on because your Grover oracle is: identify element 9, that outputs 1 for it and 0 otherwise. Having the oracle output on the qubit oracle (which is an extra qubit from the 2 registers) will mark the basis $| i, 9 \rangle$ (thank mighty superposition), and here $i$ is $4$. – cnada Mar 26 '21 at 07:25
  • @conda How i must design QRAM? Could you draw a complete execution diagram similar to the one shown in my drawing? With all quantum Operation such as H, CZ e. t. c. and QRAM? – Sergey Ivanow Mar 26 '21 at 08:27
  • @conda And to be honest, it is not clear how to read the value from memory and compare it with the desired one and how to remember the index:(( – Sergey Ivanow Mar 26 '21 at 08:29
  • @SergeyIvanow I added an image with a few steps – cnada Mar 26 '21 at 13:48
  • @conda it is greate image! How many oracles are needed and where? And what will the diffuser look like? – Sergey Ivanow Mar 26 '21 at 17:49
  • @conda I. e. Do I need to periodically manually set register 2 sequentially with values or initially fill in |0>? – Sergey Ivanow Mar 26 '21 at 18:40
  • @SergeyIvanow $\pi \sqrt{N} / 4 $ Grover iterations are required to maximize the probability of finding one element. One iteration equal one oracle plus the diffuser. Check the circuit in fig. 6.2 page 251 of http://mmrc.amss.cas.cn/tlb/201702/W020170224608149940643.pdf – cnada Mar 29 '21 at 11:06