3

$\overrightarrow f = 3x\overrightarrow i - 3y\overrightarrow j$

$\overrightarrow g = 3x\overrightarrow i + 3y\overrightarrow j$

If I calculate the divergence of $f$ I get $0$. If I calculate the divergence of $g$ I get $6$.

This seems to be saying that if the 'fluid' is flowing down it cancels out the positive horizontal flow. And if the fluid is flowing up it combines with the horizontal flow.

This doesn't seem right, we have the same magnitudes in both directions for $f$ and $g$, $g$ simply goes in the opposite direction for the $\overrightarrow j$ component. Intuitively it seems to me that for $f$ and $g$ and for any point $(x, y)$ we should have a divergence of $6$...ie. at any point, the fluid is flowing out from it as opposed to towards it?

csss
  • 3,655
  • 1
    This might be of some help: What is the meaning of evaluating the divergence at a point? – MJD Sep 18 '14 at 18:15
  • 1
    Also, have you tried sketching the vector fields in the two cases? The pictures look really different. In the second case it's clear that the arrows are all pointing outward, and that the inflow at each point (from the direction of the origin) is exceeded by the outflow at that point (in the direction away from the origin). In the first case, the inflow in the $y$ direction is exactly balanced by the outflow in the $x$ direction. – MJD Sep 18 '14 at 18:21
  • May be this question should be merged with the one you linked to, @MJD? That question (and your answer in particular) is more general making this an essential duplicate. Also editing the vector fields used here ($\vec{f}$ and $\vec{g}$) would keep it meaningful. What do you think? – Jyrki Lahtonen Sep 20 '14 at 12:30
  • @jyrki I'd be happy either way. – MJD Sep 20 '14 at 13:39

1 Answers1

5

Magnitudes of components don't tell the full story. It is also about which way they are pointing in comparison to which direction the "neighbor vectors" are pointing and how their magnitudes/directions change.

Consider your example fields plotted as vectors starting from each point.

First the vector field $\vec{f}$:

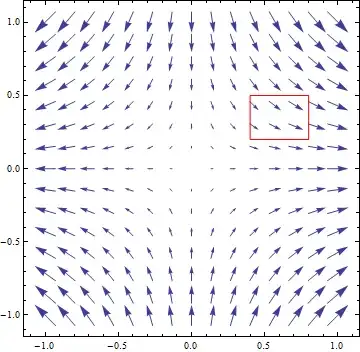
enter image description here

You see that the "flow" goes towards the $x$-axis (because the $j$-component is negative above the $x$-axes and positive below $x$-axis. Also similarly the flow goes away from $y$-axis. More to the point. If you look at a small region there is as much flow entering the region as leaving it = divergence vanishes.

For example if we look at a small region somewhere in the first quadrant (red rectangle in the figure), then there is a little bit more stuff flowing in from the top than what's exiting from the bottom (the $j$ component decreasing), but the difference is exactly compensate by left-to-right components. A little bit more is exiting from the right border than what is entering through the left border.

On the other hand the vector field $\vec{g}$ looks like the following:

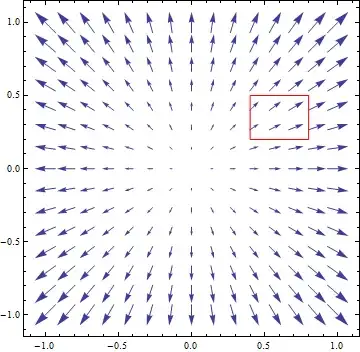
enter image description here

Here we see that the flow is aways from both axes, and actually is away from the origin. If we again look at a small rectangle somewhere in the first quadrant this time we see that the outflow through the top wins the inflow at the bottom, and ALSO the outflow to the right wins the inflow from the left. Overall more stuff is flowing out than what's entering = positive divergence.

VectorPlot[{3 x, -3 y}, {x, -1, 1}, {y, -1, 1}]

was the Mathematica command that did the first plot.

Jyrki Lahtonen
  • 133,153
  • Thanks, this is exactly the answer I wanted to write. Where did you get these flow diagrams? I tried using Wolfram|α and I was not happy with the outcome. – MJD Sep 18 '14 at 18:28
  • Cheers, I see it now, obviously there was a little bit more going on that I first thought. Would you mind posting the code for the flow diagrams so I could try out some variations myself to get a feel for them? – csss Sep 18 '14 at 18:29
  • Mathematica ver9 does these for me. Haven't done much vector calculus for a long time, so I like to play with it(will be teaching this stuff later this fall). – Jyrki Lahtonen Sep 18 '14 at 18:30