As I understand it... ahem... the (cosine, sine) vector was calculated for (30 degrees, PI/6), (45 degrees, PI/4) and (60 degrees, PI/3) angles etcetera, however, I would like know the original geometrical process for calculating the magnitudes for each vector in the trigonometric lookup table.
How did people calculate these values before calculators? Did people simple measure the adjacent and opposite lengths with accuracy?
One could probably write a whole book about this topic and the internet has several resources that help to answer the question. So summarize a few things.
Trigonometry has it's roots in astronomy. This makes good sense since angles play an important role here.
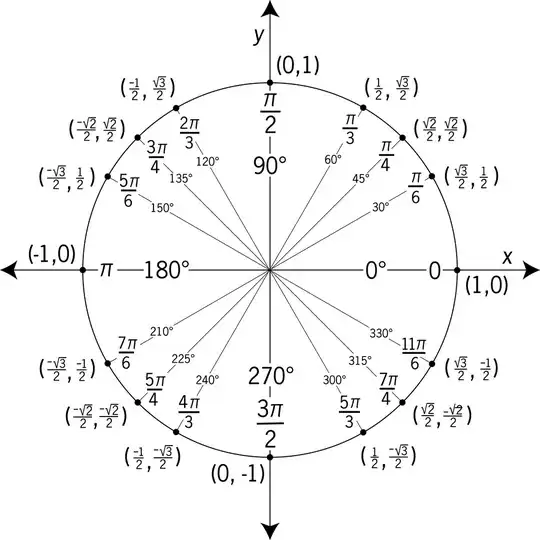
As you figured out it isn't too hard to find exactly (or approximately) the values of trigonometric functions at angles like $30^\circ, 45^\circ,$ and $60^\circ$. Using various trigonometric identities like $$\begin{align} \sin(x + y) &= \sin x \cos y + \cos x \sin y \\ a/\sin A &= b/\sin B = c/\sin C \end{align} $$ and (linear) interpolation people calculated other values. People would then create tables of values of the trigonometric functions. These tables could then be used by the "common man" for finding the values. It is, for example, a nice exercise to create a table of values of sine for multiples of $3^\circ$. For example, Ptolemy (2nd century AD) essentially created a table of values for each half degree angles.
Methods evolved and people found approximations to trigonometric functions. For example, in the 7th century AD Bhaskara I produced a formula: $$ \sin x \approx \frac{16x (\pi - x)}{5 \pi^2 - 4x (\pi - x)}, \qquad \left(0\leq x\leq\pi\right). $$
Later on more detailed tables were developed that contained values with greater accuracy.
Slide rules would contain scales for calculations of trigonometric functions. I am not sure exactly when slide rules first had trig. scales on them, but they definitely had these before the invention of the pocket calculator in the 20 century.
So in summary, the "common man" (scientist) "calculated" values of trigonometric functions before the calculator primarily using tables and slide rules. Some mathematicians where then involved in creating these tables.
A couple of reference that I used for the above are:
Here's one way I did it when I was $6$, and I'm pretty sure that this is how one could calculate it, crudely: Draw a 10 centimeter circle with center $O$, and draw a diameter $\ell$, that is, for convenience, parallel to any edge of the paper. Then, take a protractor, and mark the point $A$ where the line $\theta=\alpha$ (polar coordinates) intersects the circle $r=10$. Then, let $n$ be the line perpendicular to $\ell$ that passes though $A$, and intersects $\ell$ at $B$. Then, we have the following: $$\sin\alpha=\frac{AB}{10}\\ \cos\alpha=\frac{OB}{10}\\ \tan\alpha=\frac{AB}{OB}$$ This provides a crude approximation. For better approximations, take bigger radii. I was $6$ then, and now I'm $8$ years older, so all this is based on memory. I'm pretty sure I wrote it down right, though. (Correct me if I'm wrong.)
