The origins of these functions lies in two theorems of plane geometry that the Greeks discovered long ago:
- The sum of the angles of a triangle add up to $180^\circ$. (For the Greeks, this was "two right angles", but I'm translating into more modern terminology.)
- If two triangles have all three angles the same size as corresponding angles on the other triangle, then they are similar. That is, the ratios of corresponding sides are all the same.
So, suppose you have two right triangles. Then these two triangles each already have angles that are the same size, namely the right angle. Now suppose that they happen to have another angle with common measure. Because the sums of the three angles in each triangle add up to $180^\circ$, the third angles of each must also be the same size. Thus right triangles only need to have one other angle the same to be similar.
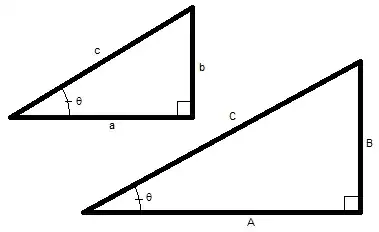
So ratios of corresponding sides of the two triangles above have to be the same:
$$\frac aA = \frac bB = \frac cC$$
A little bit of algebra gives us $$\frac ac = \frac AC,\ \ \frac bc = \frac BC,\ \ \frac ba = \frac BA$$
Label the sides by their relation to the angle $\theta$:

We see that:
for any right triangle with one of its angles equal to $\theta$, no matter what size, the ratios of $\frac {\text{adjacent}}{\text{hypotenuse}}, \frac {\text{opposite}}{\text{hypotenuse}}, \frac {\text{opposite}}{\text{adjacent}}$ are the same as for all the other such right triangles.
Thus $\theta$ completely defines these three ratios. For this reason, we give them the special names cosine, sine, and tangent.
$$\begin{align}\cos \theta &= \frac {\text{adjacent}}{\text{hypotenuse}}\\
\sin \theta &= \frac {\text{opposite}}{\text{hypotenuse}}\\
\tan \theta &= \frac {\text{opposite}}{\text{adjacent}}\end{align}$$
(The name "tangent" comes from the fact that opposite side is tangent to a circle. The name "sine" originated as the name for "half-chord", but this was abbreviated by Arabic mathematicians, then some time later after the source of this abbreviation was forgotten, was expanded again to a word meaning "cave". That word was translated back to latin "sinus", and thus to "sine". "Cosine" comes from being complementary to sine.)
So, what is the point? Because sometimes (indeed, very commonly), you can't directly measure a distance that you want to know. See that tree outside? Want to know how tall it is? If it is a big tree, directly measuring its height is a very difficult proposition.
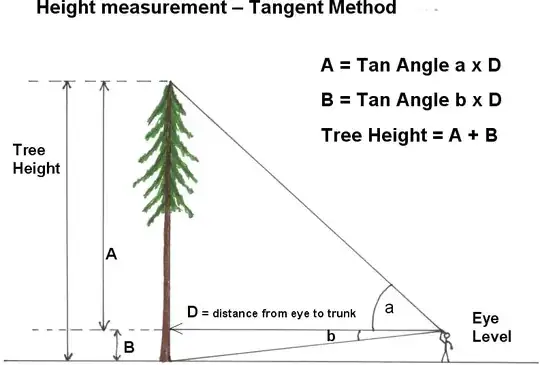
(Picture borrowed from http://www.monumentaltrees.com/en/content/measuringheight)
But if you can locate a point directly under it's tallest height, then measure the horizontal distance to some point far enough away to see the top. From that point, measure the angle your line of sight makes with the horizontal. This forms a right triangle, with the height of the tree as the opposite side, the distance you measured along the ground as the adjacent side, and the angle you measured as $\theta$. So go look up the tangent of your angle, and multiply:
$$\text{opposite} = \text{adjacent} \times \tan \theta$$
and now you know the height, without having to measure it directly. Of course, this is a simple example. In real life examples, the math is a little harder, but variants of this method allow you measure all sorts of distances where you can't get "directly under its highest point". The entire science of surveying is based on this.
So, knowing what the values of sine, cosine, and tangent are for various angles is a very, very useful thing. Now it is simple to get them. Just plug your angle into a calculator. But calculators are only about 40 years old and computers in general are less than 80 years old. Before then, mathematicians carefully worked out by hand the sine, cosine, and tangent of ranges of angles between $0^\circ$ and $90^\circ$, and listed these values in tables. To find the value for an angle not in the table, you found the nearest angles above and below, and linearly interpolated between them. Some of us who are older were taught to do that, because even though calculators existed then, they were not universal, and we were still taught the old techniques (I just missed having to learn to use a slide rule, myself.)


