Multivariate gaussian integral over positive reals

Question

The multivariate gaussian integral over the whole $\mathbf{R}^n$ has closed form solution

$$P = \int_{\mathbf{x} \in \mathbf{R}^n} \exp \left(-\frac12 \mathbf{x}^T \mathbf{A} \mathbf{x}\right)\,d\mathbf{x} = \sqrt{\frac{(2\pi)^n}{\det \mathbf{A}}}$$

where $\mathbf{A}$ is a symmetric positive-definite covariance matrix.

However, I need to solve the integral for positive reals $\{\mathbf{x} \in \mathbf{R}^n :\, \mathbf{x}_i \geq 0\ \forall i\}$ only and in at least 6 dimensions:

$$P = \int_{\{\mathbf{x} \in \mathbf{R}^n :\, \mathbf{x}_i \geq 0\ \forall i\}} \exp \left(-\frac12 \mathbf{x}^T \mathbf{A} \mathbf{x}\right)\,d\mathbf{x}$$

For diagonal $\mathbf{A}$ with zero covariance, a solution has been published. For non-diagonal covariance, my approach so far is to apply affine coordinate transforms to rotate and rescale the gaussian ellipsoid into the unit sphere (see here).

In two dimensions, the solution to the integral then reduces to comparing the area enclosed by the transformed positive coordinate axes (blue) to the area of the unit circle:

In three dimensions, the solution is given by the ration of the surface area of an enclosed spherical polygon to the surface area of the unit sphere.

In four dimensions, this approach becomes quite complicated, and I don't know how to use the usual spherical excess formulas for higher dimensions.

Any ideas or alternative approaches? Is there a multivariate error function? Any treatment on the multivariate half normal distribution?

---

Addition (2018-12-03):

Thank you Przemo for your solution to the problem for $n=2, 3$. While I had no trouble following your derivation in 2D, I'm stuck with the derivation of your intermediate step for $n=3$. I mainly tried two approaches:

• Completing the square in one variable, say $x$, leaves me with $$\int_{\mathbb{R}_+^2} \mathrm{d}y\mathrm{d}z \exp\left(-\frac{1}{2} \frac{\mathrm{det}\,A_3}{\mathrm{det}\,A_2}z^2\right) \exp\left(-\frac{1}{2} \frac{\mathrm{det}\, A_2}{a}(y-m z)^2\right) \left[1 - \mathrm{erf}\left(\frac{a_{12}y+a_{13}z}{\sqrt{2a}}\right) \right] $$ where $A_2=\begin{pmatrix} a & a_{12}\\ & b\end{pmatrix}$, $A_3$ as you defined it, and $m$ is a function of the coefficients of the matrices. However, I do not know how to proceed from there: expanding the error function to do the integral in y, say, is a nightmare due to the constant term in z; I also did not find a way to do a coordinate transform à la $s=a_{12}y+a_{13}z$ or something similar.

• Indeed, your intermediate solution looks more like you were able to complete the square in two of the variables independently; but what happened to the cross-term? I cannot find a factorisation of the exponent that would allow me to complete two integrals over the half-line with only one variable left in the error function yielded by the integral.

Any help / hint would be greatly appreciated! Thank you in advance.

Answer 1

Let us compute the result in case $n=2$. Here the matrix reads $A=\left(\begin{array}{rr}a & c\\c& b\end{array}\right)$ .Therefore we have: \begin{eqnarray} P&=& \int\limits_{{\mathbb R}_+^2} \exp\left\{-\frac{1}{2}\left[\sqrt{a}(s_1+\frac{c}{a} s_2)\right]^2 -\frac{1}{2} \frac{b a-c^2}{a} s_2^2\right\} ds_1 ds_2\\ &=&\frac{1}{\sqrt{a}} \sqrt{\frac{\pi}{2}} \int\limits_0^\infty erfc\left(\frac{c}{\sqrt{a}} \frac{s_2}{\sqrt{2}} \right)\exp\left\{-\frac{1}{2}(\frac{b a-c^2}{a})s_2^2 \right\}ds_2\\ &=&\sqrt{\frac{\pi}{2}} \frac{1}{\sqrt{b a-c^2}} \int\limits_0^\infty erfc(\frac{c}{\sqrt{b a-c^2}} \frac{s_2}{\sqrt{2}}) e^{-\frac{1}{2} s_2^2} ds_2\\ &=& \sqrt{\frac{\pi}{2}} \frac{1}{\sqrt{b a-c^2}} \left( \sqrt{\frac{\pi}{2}}- \sqrt{\frac{2}{\pi}} \arctan(\frac{c}{\sqrt{b a-c^2}})\right)\\ &=& \frac{1}{\sqrt{b a-c^2}} \arctan(\frac{\sqrt{b a-c^2}}{c}) \end{eqnarray} In the top line we completed the first integration variable to a square and in the second line we integrated over that variable. In the third line we changed variables accordingly . In the fourth line we integrated over the second variable by writing $erfc() = 1- erf()$ and then expanding the error function in a Taylor series and integrating term by term and finally in the last line we simplified the result.

Now, by doing similar calculations we obtained the following result in case $n=3$. Here $A=\left(\begin{array}{rrr}a & a_{12} & a_{13}\\a_{12}& b&a_{23}\\a_{13}&a_{23}&c\end{array}\right)$.

Firstly we have: \begin{eqnarray} &&\vec{s}^{(T)}.(A.\vec{s}) = \\ &&\left(\sqrt{a} ( s_1 + \frac{a_{1,2} s_2 + a_{1,3} s_3}{a} )\right)^2 + \left( b- \frac{a_{1,2}^2}{a}\right) s_2^2 + \left(c-\frac{a_{1,3}^2}{a}\right) s_3^2 + 2 \left(a_{2,3}-\frac{a_{1,2} a_{1,3} }{a}\right) s_2 s_3 \end{eqnarray} Therefore integrating over $s_1$ gives: \begin{eqnarray} &&P=\sqrt{\frac{\pi }{2}} \frac{1}{\sqrt{a}} \cdot \\ &&\int\limits_{{\bf R}^2} \text{erfc}\left(\frac{a_{1,2} s_2+a_{1,3} s_3}{\sqrt{2} \sqrt{a}}\right) \cdot \\ &&\exp \left[ -\frac{1}{2} \left(s_2^2 \left(b-\frac{a_{1,2}^2}{a}\right)+2 s_2 s_3 \left(a_{2,3}-\frac{a_{1,2} a_{1,3}}{a}\right)+s_3^2 \left(c-\frac{a_{1,3}^2}{a}\right)\right) \right] ds_2 ds_3=\\ && \frac{\sqrt{\pi }}{a_{1,2}} \int\limits_0^\infty \text{erfc}(u) \cdot \exp\left[-\frac{1}{2}u^2 (\frac{2 a b}{a_{1,2}^2} - 2)\right]\\ && \int\limits_0^{\frac{\sqrt{2 a}}{a_{1,3}} u} \exp \left[-\frac{1}{2} \left(s_3 u\frac{2 \sqrt{2} \sqrt{a} }{a_{1,2}} \left(a_{2,3}-\frac{b a_{1,3}}{a_{1,2}}\right)+ s_3^2\frac{a_{1,3} }{a_{1,2}} \left(\frac{a_{1,3} b}{a_{1,2}}+\frac{a_{1,2} c}{a_{1,3}}-2 a_{2,3}\right)\right)\right] ds_3 du \end{eqnarray} Now it is clear that we can do the integral over $s_3$ in the sense that we can express it through a difference of error functions.Denote $\delta:=-2 a_{1,2} a_{1,3} a_{2,3} +a_{1,3}^2 b +a_{1,2}^2 c$. Then we have

\begin{eqnarray} &&P=\frac{\pi}{\sqrt{2}\sqrt{\delta}} \cdot\int\limits_0^\infty erfc(u) \left( erf\left[\frac{\sqrt{a}(-a_{1,3} a_{2,3}+a_{1,2} c)}{a_{1,3} \sqrt{\delta}} u \right] - erf\left[ \frac{\sqrt{a}(a_{1,2} a_{2,3}-a_{1,3} b)}{a_{1,2} \sqrt{\delta}} u \right]\right) e^{-\frac{\det(A) }{\delta} u^2} du=\\ &&\frac{\pi}{\sqrt{2 \det(A)}}\cdot \\ && \int\limits_0^\infty erfc\left(u \sqrt{\frac{\delta}{\det(A)}}\right)e^{-u^2}\cdot \\ &&\left(-erfc(\sqrt{a} \frac{(-a_{13}a_{23}+a_{12} c)}{a_{13} \sqrt{\det(A)}} u)+erfc(\sqrt{a} \frac{(a_{12}a_{23}-a_{13} b)}{a_{12} \sqrt{\det(A)}} u)\right) du \\ &&=\sqrt{\frac{\pi}{2 \det(A)}}\\ \left[\right.\\ &&-\arctan\left(\frac{a_{13} \sqrt{\det(A)}}{\sqrt{a}(-a_{13}a_{23}+a_{12} c)}\right)+ \arctan\left(\frac{\sqrt{c} \sqrt{\det(A)}}{-a_{13} a_{23} + a_{12} c}\right) \\ &&+\arctan\left(\frac{a_{12} \sqrt{\det(A)}}{\sqrt{a} (a_{12} a_{23} - a_{13} b)}\right)-\arctan\left(\frac{\sqrt{b} \sqrt{\det(A)}}{a_{12} a_{23} - a_{13} b}\right) \left. \right]\\ &&=\sqrt{\frac{\pi}{2 \det(A)}}\\ &&\left[\right.\\ &&\left. \arctan\left(\frac{(a_{1,3}-\sqrt{a_{1,1}a_{3,3}})(a_{1,3}a_{2,3}-a_{1,2}a_{3,3})}{\sqrt{a_{1,1}} (a_{1,3}a_{2,3}-a_{1,2}a_{3,3})^2+a_{1,3} \sqrt{a_{3,3}} \det(A) }\sqrt{\det(A)}\right)+\right.\\ &&\left. \arctan\left(\frac{(a_{1,2}-\sqrt{a_{1,1}a_{2,2}})(a_{1,2}a_{2,3}-a_{1,3}a_{2,2})}{\sqrt{a_{1,1}} (a_{1,2}a_{2,3}-a_{1,3}a_{2,2})^2+a_{1,2} \sqrt{a_{2,2}} \det(A) }\sqrt{\det(A)}\right) \right] \end{eqnarray} where in the last line we used An integral involving error functions and a Gaussian .

I also include a Mathematica code snippet that verifies all the steps involved:

(*3d*)
A =.; B =.; CC =.; A12 =.; A23 =.; A13 =.;
For[DDet = 0, True, ,
    {A, B, CC, A12, A23, A13} = 
   RandomReal[{0, 1}, 6, WorkingPrecision -> 50];
           DDet = Det[{{A, A12, A13}, {A12, B, A23}, {A13, A23, CC}}];
     If[DDet > 0, Break[]];
  ];
a = Sqrt[(-2 A12 A13 A23 + A13^2 B + A12^2 CC)/DDet];
{b1, b2} = {( Sqrt[A]  (-A13 A23 + A12 CC))/ Sqrt[DDet], ( 
   Sqrt[A] (A12 A23 - A13 B))/ Sqrt[DDet]};
{AA1, AA2} = {2 Sqrt[2] Sqrt[
    A] (( A23 A12 - A13 B)/A12^2), (-2 A12 A13 A23 + A13^2 B + 
    A12^2 CC)/A12^2};

{DDet, a, b1, b2};
NIntegrate[
 Exp[-1/2 (A s1^2 + B s2^2 + CC s3^2 + 2 A12 s1 s2 + 2 A23 s2 s3 + 
     2 A13 s1 s3)], {s1, 0, Infinity}, {s2, 0, Infinity}, {s3, 0, 
  Infinity}]
NIntegrate[
 Exp[-1/2 ((Sqrt[A] (s1 + (A12 s2 + A13 s3)/A))^2 + (B - 
        A12^2/A) s2^2 + (CC - A13^2/A) s3^2 + 
     2 (A23 - A12 A13/A) s2 s3)], {s1, 0, Infinity}, {s2, 0, 
  Infinity}, {s3, 0, Infinity}]
NIntegrate[
 1/Sqrt[A] Sqrt[
   Pi/2] Erfc[(A12 s2 + A13 s3)/
    Sqrt[2 A]] Exp[-1/
     2 ((B - A12^2/A) s2^2 + (CC - A13^2/A) s3^2 + 
      2 (A23 - A12 A13/A) s2 s3)], {s2, 0, Infinity}, {s3, 0, 
  Infinity}]
 Sqrt[Pi]/A12 NIntegrate[  
  Erfc[u] Exp[-1/
      2 ( A13/A12 (-2 A23 + (A13 B)/A12 + CC A12/A13) s3^2 + (
        2 Sqrt[2] Sqrt[A] )/
        A12 ( A23 - ( A13 B)/A12) s3 u + (-2 + (2 A B)/
          A12^2) u^2)], {u, 0, Infinity}, {s3, 0, Sqrt[2 A]/A13 u}]
 Sqrt[Pi]/A12 NIntegrate[  
  Erfc[u] Exp[-1/2 (Sqrt[AA2] s3 + u/2 AA1/Sqrt[AA2])^2] Exp[-((
     DDet u^2)/(-2 A12 A13 A23 + A13^2 B + A12^2 CC))], {u, 0, 
   Infinity}, {s3, 0, Sqrt[2 A]/A13 u}]
 Sqrt[Pi]/(A12 Sqrt[AA2])
  NIntegrate[  
  Erfc[u] Exp[-1/2 (s3)^2] Exp[-((
     DDet u^2)/(-2 A12 A13 A23 + A13^2 B + A12^2 CC))], {u, 0, 
   Infinity}, {s3, 
   u/2 AA1/Sqrt[AA2], ((A13 AA1 + 2 AA2 Sqrt[2] Sqrt[A]) u)/(
   2 A13 Sqrt[AA2])}]
 Sqrt[Pi]/(A12 Sqrt[AA2]) Sqrt[\[Pi]/2]
  NIntegrate[  
  Erfc[u] ( 
    Erf[(A13 AA1 + 2 AA2 Sqrt[2] Sqrt[A])/(2 A13 Sqrt[2] Sqrt[AA2])
        u] - Erf[AA1/(2 Sqrt[2] Sqrt[AA2]) u]) Exp[-((
     DDet u^2)/(-2 A12 A13 A23 + A13^2 B + A12^2 CC))], {u, 0, 
   Infinity}]
 Pi/Sqrt[-2 A12 A13 A23 + A13^2 B + A12^2 CC] Sqrt[1/2]
  NIntegrate[  
  Erfc[u] ( 
    Erf[( Sqrt[A] (-A13 A23 + A12 CC) u)/(
      A13 Sqrt[-2 A12 A13 A23 + A13^2 B + A12^2 CC])] - 
     Erf[(Sqrt[A] (A12 A23 - A13 B) u)/(
      A12 Sqrt[-2 A12 A13 A23 + A13^2 B + A12^2 CC])]) Exp[-((
     DDet u^2)/(-2 A12 A13 A23 + A13^2 B + A12^2 CC))], {u, 0, 
   Infinity}]
Pi/ Sqrt[-2 A12 A13 A23 + A13^2 B + 
   A12^2 CC] Sqrt[1/2] a NIntegrate[  
  Erfc[a u] ( 
    Erf[( Sqrt[A] (-A13 A23 + A12 CC) u)/(A13 Sqrt[DDet])] - 
     Erf[(Sqrt[A] (A12 A23 - A13 B) u)/(A12 Sqrt[DDet])]) Exp[- 
     u^2], {u, 0, Infinity}]
Pi/Sqrt[2 DDet] NIntegrate[(Erfc[u a]) Exp[-u^2] (Erf[b1/A13 u] - 
     Erf[b2/A12 u]), {u, 0, Infinity}]
Sqrt[Pi]/Sqrt[
  2 DDet] (ArcTan[ Sqrt[A]/A13   (-A13 A23 + A12 CC)/ Sqrt[DDet]] - 
   ArcTan[1/ Sqrt[CC]    (-A13 A23 + A12 CC)/ Sqrt[DDet]] - 
   ArcTan[ Sqrt[A]/A12  (A12 A23 - A13 B)/ Sqrt[DDet]] + 
   ArcTan[ 1/Sqrt[B]   (A12 A23 - A13 B)/ Sqrt[DDet]])
-(Sqrt[Pi]/
  Sqrt[2 DDet]) (ArcTan[(A13 Sqrt[DDet])/(
    Sqrt[A] (-A13 A23 + A12 CC))] - 
   ArcTan[(Sqrt[CC] Sqrt[DDet])/(-A13 A23 + A12 CC)] - 
   ArcTan[(A12 Sqrt[DDet])/(Sqrt[A] (A12 A23 - A13 B))] + 
   ArcTan[(Sqrt[B] Sqrt[DDet])/(A12 A23 - A13 B)])
Sqrt[Pi]/Sqrt[
  2 DDet] (ArcTan[((A13 - Sqrt[A] Sqrt[CC]) (A13 A23 - A12 CC) Sqrt[
     DDet])/(Sqrt[A] (A13 A23 - A12 CC)^2 + A13 Sqrt[CC] DDet)] + 
   ArcTan[((A12 - Sqrt[A] Sqrt[B]) (A12 A23 - A13 B) Sqrt[DDet])/(
    Sqrt[A] (A12 A23 - A13 B)^2 + A12 Sqrt[B] DDet)])

Update: Now let us take a look at the $n=4$ case. In here: \begin{equation} {\bf A}=\left( \begin{array}{rrrr} a & a_{1,2} & a_{1,3} & a_{1,4} \\ a_{1,2} & b & a_{2,3} & a_{2,4} \\ a_{1,3} & a_{2,3} & c & a_{3,4} \\ a_{1,4} & a_{2,4} & a_{3,4} & d \end{array} \right) \end{equation}

then by doing basically the same computations as a above we managed to reduce the integral in question to a following two dimensional integral. We have: \begin{eqnarray} &&P= \\ &&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\frac{\pi}{\sqrt{2 \delta}} \int\limits_0^\infty \int\limits_0^{\frac{\sqrt{2 a}}{a_{1,2}} u} erfc[u] \cdot \exp\left[\frac{{\mathfrak A}_{0,0} u^2 + {\mathfrak A}_{1,0} u s_2 +{\mathfrak A}_{1,1} s_2^2}{2 \delta}\right] \cdot \left( erf[\frac{{\mathfrak B}_1 u + {\mathfrak B}_2 s_2}{a_{1,3} \sqrt{2 \delta}}] + erf[\frac{{\mathfrak C}_1 u + {\mathfrak C}_2 s_2}{a_{1,4} \sqrt{2 \delta}}]\right) d s_2 du=\\ &&\frac{2 \imath \pi^{3/2}}{\sqrt{{\mathfrak A}_{1,1}}} \int\limits_0^\infty erfc[u] \exp\{\frac{4 {\mathfrak A}_{0,0} {\mathfrak A}_{1,1} - {\mathfrak A}_{1,0}^2}{8\delta {\mathfrak A}_{1,1}} u^2\}\cdot\\ && \left[\right.\\ &&\left. \left.T\left(\frac{({\mathfrak A}_{1,0}+\xi) u}{2\imath \sqrt{{\mathfrak A}_{1,1} \delta}}, \frac{\imath {\mathfrak B}_2}{a_{1,3} \sqrt{{\mathfrak A}_{1,1}}},\frac{u(2{\mathfrak A}_{1,1} {\mathfrak B}_1 - {\mathfrak A}_{1,0} {\mathfrak B}_2)}{2\sqrt{\delta} a_{1,3} {\mathfrak A}_{1,1}}\right)\right|_{\frac{2{\mathfrak A}_{1,1} \sqrt{2 a}}{a_{1,2}}}^0 +\right.\\ &&\left. \left.T\left(\frac{({\mathfrak A}_{1,0}+\xi) u}{2\imath \sqrt{{\mathfrak A}_{1,1} \delta}}, \frac{\imath {\mathfrak C}_2}{a_{1,3} \sqrt{{\mathfrak A}_{1,1}}},\frac{u(2{\mathfrak A}_{1,1} {\mathfrak C}_1 - {\mathfrak A}_{1,0} {\mathfrak C}_2)}{2\sqrt{\delta} a_{1,3} {\mathfrak A}_{1,1}}\right)\right|_{\frac{2{\mathfrak A}_{1,1} \sqrt{2 a}}{a_{1,2}}}^0 +\right.\\ &&\left. \right] du \quad (i) \end{eqnarray} where $T(\cdot,\cdot,\cdot)$ is the generalized Owen's T function Generalized Owen's T function and \begin{eqnarray} \delta&:=&a_{1,3}(a_{1,3} d-a_{1,4} a_{3,4}) + a_{1,4}(a_{1,4} c- a_{1,3} a_{3,4})\\ {\mathfrak A}_{0,0}&:=&2 a \left(a_{3,4}^2-c d\right)+2 a_{1,4} (a_{1,4} c-a_{1,3} a_{3,4})+2 a_{1,3} (a_{1,3} d-a_{1,4} a_{3,4})\\ {\mathfrak A}_{1,0}&:=&2 \sqrt{2} \sqrt{a} \left(a_{1,2} \left(c d-a_{3,4}^2\right)+a_{1,3} (a_{2,4} a_{3,4}-a_{2,3} d)+a_{1,4} (a_{2,3} a_{3,4}-a_{2,4} c)\right)\\ {\mathfrak A}_{1,1}&:=&a_{1,2}^2 \left(a_{3,4}^2-c d\right)+2 a_{1,2} a_{1,3} (a_{2,3} d-a_{2,4} a_{3,4})+2 a_{1,2} a_{1,4} (a_{2,4} c-a_{2,3} a_{3,4})+a_{1,3}^2 \left(a_{2,4}^2-b d\right)+2 a_{1,3} a_{1,4} (a_{3,4} b-a_{2,3} a_{2,4})+a_{1,4}^2 \left(a_{2,3}^2-b c\right)\\ \hline\\ {\mathfrak B}_1&:=&\sqrt{2} \sqrt{a} (a_{1,4} c-a_{1,3} a_{3,4})\\ {\mathfrak B}_2&:=&a_{1,2} (a_{1,3} a_{3,4}-a_{1,4} c)+a_{1,3} (a_{1,4} a_{2,3}-a_{1,3} a_{2,4})\\ {\mathfrak C}_1&:=&\sqrt{2} \sqrt{a} (a_{1,3} d-a_{1,4} a_{3,4})\\ {\mathfrak C}_2&:=&a_{1,2} (a_{1,4} a_{3,4}-a_{1,3} d)+a_{1,4} (a_{1,3} a_{2,4}-a_{1,4} a_{2,3}) \end{eqnarray}

nu = 4; Clear[T]; Clear[a]; x =.;
(*a0.dat, a1.dat or a2.dat*)
mat = << "a0.dat";
{a, b, c, d, a12, a13, a14, a23, a24, a34} = {mat[[1, 1]], 
   mat[[2, 2]], mat[[3, 3]], mat[[4, 4]], mat[[1, 2]], mat[[1, 3]], 
   mat[[1, 4]], mat[[2, 3]], mat[[2, 4]], mat[[3, 4]]};
{dd, A00, A10, 
   A11} = {-2 a13 a14 a34 + a14^2 c + a13^2 d, -4 a13 a14 a34 + 
    2 a a34^2 + 2 a14^2 c + 2 a13^2 d - 2 a c d, 
   2 Sqrt[2] Sqrt[a] a14 a23 a34 + 2 Sqrt[2] Sqrt[a] a13 a24 a34 - 
    2 Sqrt[2] Sqrt[a] a12 a34^2 - 2 Sqrt[2] Sqrt[a] a14 a24 c - 
    2 Sqrt[2] Sqrt[a] a13 a23 d + 2 Sqrt[2] Sqrt[a] a12 c d, 
   a14^2 a23^2 - 2 a13 a14 a23 a24 + a13^2 a24^2 - 
    2 a12 a14 a23 a34 - 2 a12 a13 a24 a34 + a12^2 a34^2 + 
    2 a13 a14 a34 b + 2 a12 a14 a24 c - a14^2 b c + 2 a12 a13 a23 d - 
    a13^2 b d - a12^2 c d};
{B1, B2, C1, 
   C2} = {Sqrt[2] Sqrt[
    a] (-a13 a34 + a14 c), (a13 a14 a23 - a13^2 a24 + a12 a13 a34 - 
     a12 a14 c), 
   Sqrt[2] Sqrt[
    a] (-a14 a34 + a13 d), (-a14^2 a23 + a13 a14 a24 + a12 a14 a34 - 
     a12 a13 d)};
NIntegrate[
 Exp[-1/2 Sum[mat[[i, j]] s[i] s[j], {i, 1, nu}, {j, 1, nu}]], 
 Evaluate[Sequence @@ Table[{s[eta], 0, Infinity}, {eta, 1, nu}]]]
Sqrt[\[Pi]/(2 a)]
  NIntegrate[ 
  Erfc[(a12 s[2] + a13 s[3] + a14 s[4])/Sqrt[
    2 a]] Exp[-1/
      2 ((-(a12^2/a) + b) s[2]^2 + (-(a13^2/a) + c) s[
         3]^2 + (-(a14^2/a) + d) s[4]^2 + 
       2 (-(( a13 a14)/a) + a34) s[3] s[4] + 
       2 (-(( a12 a13)/a) + a23) s[2] s[3] + 
       2 (-(( a12 a14)/a) + a24) s[2] s[4])], 
  Evaluate[Sequence @@ Table[{s[eta], 0, Infinity}, {eta, 2, nu}]]]

Sqrt[\[Pi]]
  1/a14 NIntegrate[ 
  Erfc[u] Exp[(
     2 a14 a24 s[2] (-Sqrt[2] Sqrt[a] u + a12 s[2]) - 
      d (2 a u^2 - 2 Sqrt[2] Sqrt[a] a12 u s[2] + a12^2 s[2]^2) + 
      a14^2 (2 u^2 - b s[2]^2))/(
     2 a14^2) + ((Sqrt[2] Sqrt[
         a] (-a14 a34 + a13 d) u + (-a14^2 a23 + a13 a14 a24 + 
           a12 a14 a34 - a12 a13 d) s[2]) s[3])/
     a14^2 - ((-2 a13 a14 a34 + a14^2 c + a13^2 d) s[3]^2)/(
     2 a14^2)], {u, 0, Infinity}, {s[2], 0, 
   Sqrt[2] Sqrt[a]/a12 u}, {s[3], 0, (Sqrt[2 a] u - a12 s[2])/a13}]
 Pi/Sqrt[2 dd]
  NIntegrate[ 
  Erfc[u] Exp[(A00 u^2 + A10 u s[2] + A11 s[2]^2)/(
    2 (dd))]  (Erf[(B1 u + B2 s[2])/( a13 Sqrt[2 dd])] + 
     Erf[(C1 u + C2 s[2])/( a14^1 Sqrt[2 dd])]), {u, 0, 
   Infinity}, {s[2], 0, Sqrt[2] Sqrt[a]/a12 u}]

Now, I will provide the result. Note that the only assumptions on the underlying matrix ${\bf A}$ are that it is symmetric and that its elements are non-negative. Firstly let us define: \begin{eqnarray} &&{\mathfrak J}^{(1,1)}(a,b,c)= \frac{1}{\pi^2}\cdot \left(\right.\\ &&\left. -\frac{1}{8} \sum\limits_{i=1}^4 \sum\limits_{j=1}^4 (-1)^{j-1+\lfloor \frac{i-1}{2} \rfloor } % {\mathfrak F}^{(1,\frac{\sqrt{1+2 a^2+b^2} - \sqrt{2} a}{\sqrt{1+b^2}})}_{\frac{i \sqrt{b^2 c^2+b^2+1} (-1)^{\left\lfloor \frac{j-1}{2}\right\rfloor }+i b c (-1)^j}{\sqrt{b^2+1}},-\frac{b (-1)^i+i (-1)^{\left\lceil \frac{i-1}{2}\right\rceil }}{\sqrt{b^2+1}}} % \right. \\ &&\left. \right)\quad (ii) \end{eqnarray} where ${\mathfrak F}^{(A,B)}_{a,b}$ is related to di-logarithms and is defined in An integral involving a Gaussian, error functions and the Owen's T function. . Then we define another function as follows: \begin{equation} {\bar {\mathfrak J}}^{(1,1)}(a,b,c):= \frac{\pi}{2} \arctan\left[ \frac{\sqrt{2 a} c}{\sqrt{2 a+b^2(1+c^2)}}\right] - \frac{\pi}{2} \arctan\left[ c\right] - 2 \pi^2 {\mathfrak J}^{(1,1)}(\frac{1}{\sqrt{2 a}},\frac{b}{\sqrt{2 a}},c) \end{equation} and then the following quantities that depend on the underlying matrix. We have: \begin{eqnarray} \delta&:=& a_{3,3} a_{4,1}^2 - 2 a_{3,1} a_{3,4} a_{4,1} + a_{4,4} a_{3,1}^2\\ W&:=&\left(a_{3,3} a_{4,4}-a_{3,4}^2\right) a_{1,2}^2+2 a_{1,4} (a_{2,3} a_{3,4}-a_{2,4} a_{3,3}) a_{1,2}+2 a_{1,3} (a_{2,4} a_{3,4}-a_{2,3} a_{4,4}) a_{1,2}+a_{1,4}^2 \left(a_{2,2} a_{3,3}-a_{2,3}^2\right)+2 a_{1,3} a_{1,4} (a_{2,3} a_{2,4}-a_{2,2} a_{3,4})+a_{1,3}^2 \left(a_{2,2} a_{4,4}-a_{2,4}^2\right)\\ W_1&:=&2 \sqrt{a_{1,1}} \left(a_{1,4} (a_{2,4} a_{3,3}-a_{2,3} a_{3,4})+a_{1,3} (a_{2,3} a_{4,4}-a_{2,4} a_{3,4})+a_{1,2} \left(a_{3,4}^2-a_{3,3} a_{4,4}\right)\right)\\ % v_1&:=&\frac{1}{a_{4,1} \sqrt{\delta}} \left( \sqrt{a_{1,1}}(a_{3,4} a_{4,1} - a_{3,1} a_{4,4}),-a_{2,4} a_{3,1} a_{4,1} + a_{2,3} a_{4,1}^2+a_{2,1}(-a_{3,4} a_{4,1}+a_{3,1}a_{4,4})\right)\\ v_2&:=&-\frac{1}{a_{3,1} \sqrt{\delta}} \left(\sqrt{a_{1,1}}(a_{3,4} a_{3,1} - a_{4,1} a_{3,3}),-a_{3,1} a_{3,2} a_{4,1} +a_{2,4} a_{3,1}^2 + a_{2,1}(-a_{3,4} a_{3,1}+a_{4,1}a_{3,3}) \right)\\ % \left( A, B \right)&:=& \frac{1}{\delta} \left( W,W_1 \right)\\ \left( {\bf a}_1,{\bf a}_2 \right)&:=& \frac{1}{\sqrt{A}} \left(v_1(2),v_2(2) \right)\\ {\bf b}_1&:=& \sqrt{2} v_1(1) - \frac{B}{\sqrt{2} A} v_1(2)\\ {\bf b}_2&:=& \sqrt{2} v_2(1) - \frac{B}{\sqrt{2} A} v_2(2)\\ x&:=& \frac{\sqrt{a_{1,1}}}{a_{2,1}} \end{eqnarray} Then the result reads: \begin{eqnarray} &&P=\frac{1}{\det({\bf A})} \left(\right.\\ % && {\bar {\mathfrak J}}^{(1,1)}\left( \frac{\det({\bf A})}{W},\frac{B}{\sqrt{2 A}},{\bf a}_2+\frac{\sqrt{2 A} {\bf b}_2}{B}\right) - {\bar {\mathfrak J}}^{(1,1)}\left( \frac{\det({\bf A})}{W},\frac{B+2 A x}{\sqrt{2 A}},{\bf a}_2+\frac{\sqrt{2 A} {\bf b}_2}{B+2 A x}\right)+\\ &&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! {\bar {\mathfrak J}}^{(1,1)}\left( \frac{\det({\bf A})}{W},\frac{{\bf b}_2}{\sqrt{1+{\bf a}_2^2}},{\bf a}_2+\frac{B(1+{\bf a}_2^2)}{\sqrt{2 A}{\bf b}_2}\right) - {\bar {\mathfrak J}}^{(1,1)}\left( \frac{\det({\bf A})}{W},\frac{{\bf b}_2}{\sqrt{1+{\bf a}_2^2}},{\bf a}_2+\frac{(B+2 A x)(1+{\bf a}_2^2)}{\sqrt{2 A}{\bf b}_2}\right)+\\ % && -{\bar {\mathfrak J}}^{(1,1)}\left( \frac{\det({\bf A})}{W},\frac{B}{\sqrt{2 A}},{\bf a}_1+\frac{\sqrt{2 A} {\bf b}_1}{B}\right) + {\bar {\mathfrak J}}^{(1,1)}\left( \frac{\det({\bf A})}{W},\frac{B+2 A x}{\sqrt{2 A}},{\bf a}_1+\frac{\sqrt{2 A} {\bf b}_1}{B+2 A x}\right)+\\ &&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! -{\bar {\mathfrak J}}^{(1,1)}\left( \frac{\det({\bf A})}{W},\frac{{\bf b}_1}{\sqrt{1+{\bf a}_1^2}},{\bf a}_1+\frac{B(1+{\bf a}_1^2)}{\sqrt{2 A}{\bf b}_1}\right) + {\bar {\mathfrak J}}^{(1,1)}\left( \frac{\det({\bf A})}{W},\frac{{\bf b}_1}{\sqrt{1+{\bf a}_1^2}},{\bf a}_1+\frac{(B+2 A x)(1+{\bf a}_1^2)}{\sqrt{2 A}{\bf b}_1}\right)\\ % &&\left.\right) \end{eqnarray} I can provide a code for testing the above expression if anyone is interested.

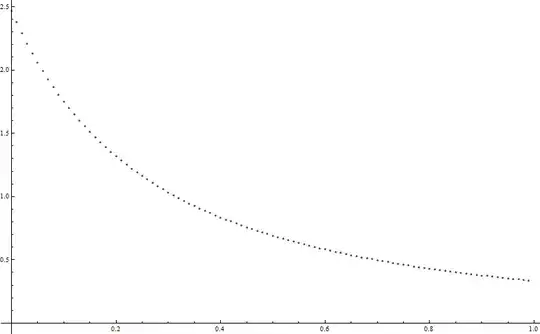
Now, in the particular case when all the diagonal elements of the matrix ${\bf A}$ are equal unity and all the cross diagonal terms are equal to $\rho$ where $0 \le \rho \le 1$ then the result reads:

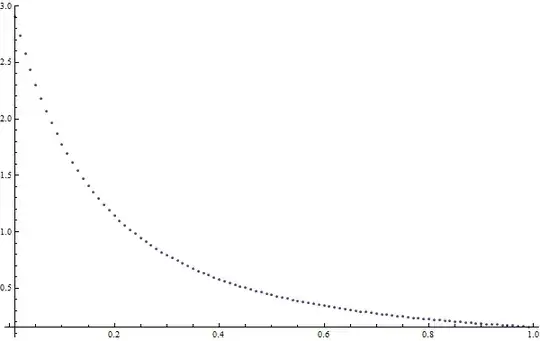
\begin{eqnarray} &&P=\\ &&\frac{2 \pi ^{3/2}}{\sqrt{(1-\rho )^3 (3 \rho +1)}} \left( \frac{\pi -3 \arctan\left(\sqrt{\frac{3 \rho +1}{\rho +1}}\right)}{2 \sqrt{\pi }} +6\sqrt{\pi} {\mathfrak J}^{(1,1)}\left( \frac{\sqrt{\frac{3}{2}} \rho }{\sqrt{(1-\rho ) (3 \rho +1)}},\frac{\sqrt{1-\rho }}{\sqrt{2} \sqrt{(1-\rho ) (3 \rho +1)}},\sqrt{3}\right)\right) \end{eqnarray} Below I plot the quantity $P$ as a function of $\rho$. Note that the value $P(\rho=0) = \pi^2/4 \simeq 2.4674$ as it is.

Answer 2

The integral over (coordinate-wise) positive values appears in the treatment of dichotomized Gaussian distributions, so you might find the answer to your problem there. Relevant references would be:

• DR Cox, N Wermuth, Biometrika, 2002
• JH Macke, P Berens et al., Neural Computation, 2009

Answer 3

Other names for this quantity are the "multivariate Gaussian cumulative distribution", the "normalization constant of the truncated normal distribution", "non-centered orthant probabilities", ...

There appears to be a rather extensive literature on this. See for example The Normal Law Under Linear Restrictions: Simulation and Estimation via Minimax Tilting and many citations therein, like this one

Here is a paper that has closed-form expressions for the orthant probabilities for $n=4$, under different sets of assumptions for the covariance matrix.

I will update this answer as I learn more about it

Answer 4

For Przemo's example with $n=5$, define a higher arcsine:

$$\arcsin(a,b,c) = \int_0^b \frac { \arcsin\left( a \beta c / v / w \right) } { \sqrt{1-\beta^2} } d\beta$$

$$\text{where}\; v = \sqrt{ 1-a^2-\beta^2 },\; w = \sqrt{ 1-\beta^2-c^2 },$$

and the orthoscheme volume:

$$V( a, b, c, d ) = \frac {\pi^2} {60} + \frac {\pi} {30} \left( \arcsin( a ) + \arcsin( b ) + \arcsin( c ) + \arcsin( d ) \right) + \frac {1} {15} \left( \arcsin( a ) \arcsin( c ) + \arcsin( a ) \arcsin( d ) + \arcsin( b ) \arcsin( d ) + \arcsin( a, b, c ) + \arcsin( b, c, d ) \right) .$$

Then the (normalized) orthant probability for A is $\frac{15S}{8\pi^2}$ where:

$$ S = 8 \cdot V \left( abc, -\sqrt{\frac{1-a}{2}}, -\frac{1+a-2ab}{2(1-ab)}, -\frac{1-a}{2(1-ab)} \right) \\ + 16 \cdot V \left( abc, -\sqrt{\frac{1-ab}{2}}, -\frac{1}{2}\sqrt{\frac{1-a}{1-ab}}, -\frac{1}{2}\sqrt{\frac{1+a-2ab}{1-ab}} \right) . $$

E.g., for $a = 0.3, b = 0.2, c = 0.1$, we get $\approx 0.049972036321177378010658463826149025346$.

Answer 5

Here we provide an answer for $n=5$ in case when the underlying matrix ${\bf A}$ has the following form: \begin{eqnarray} {\bf A}= \left( \begin{array}{ccccc} 1 & a & a b c & a b & a b \\ a & 1 & a b c & a b & a b \\ a b c & a b c & 1 & a b c & a b c \\ a b & a b & a b c & 1 & a \\ a b & a b & a b c & a & 1 \\ \end{array} \right) \end{eqnarray} where $a\in(0,1)$,$b\in(0,1)$ and $c\in(0,1)$

We have derived the result basically in the same way as in my previous answer above, meaning by firstly bringing the quadratic form to a square in one variable and integrating over that variable and then by successively integrating over the remaining variables and reducing the dimension of the integral. Firstly let us note that the function ${\mathfrak J}^{(1,1)}$ is defined as in my previous answer above and then let us also define the following: \begin{equation} {\mathfrak J}^{(2,1)}\left( (a_1,a_2), b, c\right):= \int\limits_0^\infty \frac{e^{-1/2 \xi^2}}{\sqrt{2 \pi}} \cdot [\prod\limits_{j=1}^2 erf(a_j \xi)] \cdot T(b \xi, c) d\xi \end{equation} This function can be always reduced to di-logarithms as shown in An integral involving a Gaussian, error functions and the Owen's T function. .

Now we define the following auxiliary quantities: \begin{eqnarray} \delta&:=&2+(1+a-4 a b) c^2\\ \delta_1&:=&1-a+(1+a(1+2 b(-2+a b))) c^2\\ \delta_2&:=&1+a(1+2 b)-4 a^2b^2 c^2\\ \delta_3&:=&1+(1-2 a b)c^2\\ \delta_4^{(-)}&:=&1+a(1-2 b)\\ \delta_4^{(+)}&:=&1+a(1+2 b)\\ \delta_5&:=&1+a(1+a b^2(-2+(-3+a(-1+4 b))c^2))\\ \delta_6&:=&1-a b c^2\\ \hline\\ (A,A_1,A_2)&:=& \left( \frac{c(1-a b)\sqrt{\delta}}{\delta_6 \sqrt{1-a}}, \frac{\sqrt{\delta (1-a)}}{c \delta_4^{(-)}}, \frac{1}{c} \sqrt{\frac{\delta}{1-a}}\right)\\ A_3&:=& \frac{a b \sqrt{(1-a) \delta}}{\sqrt{2 \delta_4^{(-)} \delta_2}}\\ (A_4,A_5)&:=& \left( \frac{\sqrt{2} \sqrt{1-a^2} \delta_6}{\sqrt{\delta_4^{(-)} \delta_2 \delta_3}}, \frac{\sqrt{1+a} \sqrt{\delta_4^{(-)}} c}{\sqrt{\delta_2}} \right)\\ (A_6,A_7,A_8)&:=& \left( \frac{\sqrt{\delta_4^{(-)} \delta_2}}{\sqrt{2 \delta_5}}, \frac{(1-a b) c \sqrt{\delta_4^{(-)} \delta_2}}{\sqrt{\delta_1 \delta_5}}, \frac{\sqrt{\delta_2 (1-a)}}{\sqrt{\delta_4^{(+)} \delta_1}} \right)\\ A_9&:=& \sqrt{\frac{1+a}{1-a}} \end{eqnarray} Then the result reads: \begin{eqnarray} &&P=\frac{2^{3/2} \pi}{\sqrt{(1-a)^2 \delta_4^{(m)} \delta_2}} \cdot \left(\right.\\ && \frac{1}{2 \sqrt{\pi}} \left( -\pi(\arcsin(A_6)+\arcsin(A_7)+\arcsin(A_8)) + (\pi-2 \arcsin(A_6))(\arctan(A)+\arctan(A_1)+\arctan(A_2))\right) + \\ && 2 \pi^{3/2} \left( {\mathfrak J}^{(1,1)}(A_3,\frac{A_4}{\sqrt{2}},A_2) + {\mathfrak J}^{(1,1)}(A_3,\frac{A_5}{\sqrt{2}},A_1) + {\mathfrak J}^{(1,1)}(A_3,\frac{A_4}{\sqrt{2}},A)\right) +\\ && 2 \pi^{3/2} \left( {\mathfrak J}^{(2,1)}\left( (\frac{1}{A_4},\frac{A_2}{\sqrt{2}}),\frac{2 A_3}{A_4}, A_9\right) + {\mathfrak J}^{(2,1)}\left( (\frac{1}{A_4},\frac{A}{\sqrt{2}}),\frac{2 A_3}{A_4}, A_9\right) + {\mathfrak J}^{(2,1)}\left( (\frac{1}{A_5},\frac{A_1}{\sqrt{2}}),\frac{2 A_3}{A_5}, A_9\right) \right)+\\ &&\!\!\!\!\!\!\!\!\!\! 2 \pi^{3/2} \left( {\mathfrak J}^{(2,1)}\left( (\frac{1}{2 A_3},\frac{A_9}{\sqrt{2}}),\frac{A_4}{2 A_3},A_2\right)+ {\mathfrak J}^{(2,1)}\left( (\frac{1}{2 A_3},\frac{A_9}{\sqrt{2}}),\frac{A_5}{2 A_3},A_1\right)+ {\mathfrak J}^{(2,1)}\left( (\frac{1}{2 A_3},\frac{A_9}{\sqrt{2}}),\frac{A_4}{2 A_3},A\right) \right)\\ \left. \right) \end{eqnarray}

Again, I have a code for testing this expression if anyone was interested.

Now, in the limit $b=c=1$ we have $(A,A_1,A_2)=(\sqrt{3},\sqrt{3},\sqrt{3})$, $A_3=\sqrt{3} a/(\sqrt{2+8 a})$, $(A_4,A_5)=(\sqrt{(1+a)/(1+4 a)},\sqrt{(1+a)/(1+4 a)})$ and $(A_6,A_7,A_8)=(\sqrt{(1+4 a)/(2+6 a)},\sqrt{(1+4 a)/(2+6 a)},\sqrt{(1+4 a)/(2+6 a)})$ and then we have: \begin{eqnarray} &&P=\frac{2^{3/2} \pi}{\sqrt{(1-a)^4(1+4 a)}}\left(\right.\\ &&\frac{\pi}{2\sqrt{\pi}} \left(\pi - 5 \arcsin(\sqrt{\frac{1+4 a}{2+6 a}}) \right) \\ && 6 \pi^{3/2} {\mathfrak J}^{(1,1)}\left( \frac{\sqrt{\frac{3}{2}} a }{\sqrt{4 a +1}},\frac{\sqrt{\frac{a +1}{4 a +1}}}{\sqrt{2}},\sqrt{3}\right)+\\ && 6 \pi^{3/2} {\mathfrak J}^{(2,1)}\left((\sqrt{\frac{3}{2}},\sqrt{\frac{4 a +1}{a +1}}),\frac{\sqrt{6} a }{\sqrt{a +1}},\frac{a +1}{\sqrt{1-a ^2}} \right)+\\ && 6 \pi^{3/2} {\mathfrak J}^{(2,1)}\left((\frac{\sqrt{4 a +1}}{\sqrt{6} a },\frac{a +1}{\sqrt{2} \sqrt{1-a ^2}}),\frac{\sqrt{a +1}}{\sqrt{6} a },\sqrt{3} \right) \\ \left.\right)\\ \end{eqnarray} Below I plot the quantity in question as a function of $a$. Note that the value $P(a=0)= (\sqrt{\pi}/\sqrt{2})^5 \simeq 3.09243$ as it is.

Answer 6

There is a solution in the form of a Taylor series.

See this Wikipedia page which refers to "Measuring Solid Angles Beyond Dimension Three" by Jason M. Ribando (DOI: 10.1007/s00454-006-1253-4).

For that Taylor series you get (Lemma 2.1 from Ribando) for a matrix $\mathbf{A} = (\alpha_{ij})$

$$\exp \left(-\frac12 \mathbf{x}^T \mathbf{A} \mathbf{x}\right) = \sum_{\mathbf{a} \in N^{{n}\choose{2}}} \left[ \frac{(-2)^{\sum_{i<j} a_{ij}}}{\prod_{i<j} a_{ij}!} \prod_{l=1}^n x_{l}^{\sum_{m \neq l} a_{lm}} \prod_{i} e^{-x_{i}^2} \right] \boldsymbol{\alpha}^{\mathbf{a}}$$

Where the subscript $i<j$ means that we sum over one half of the off-diagonal elements, and the subscript $m \neq l$ means that we sum over all cases in this half of the off-diagonal elements where either the first or the second subscript is equal to $l$ (This was not intuitive to me at first but say $l=3$ then the set $a_{31}, a_{32}, a_{34}, a_{35}, \dots a_{3n}$ is equal to $a_{13}, a_{23}, a_{34}, a_{35}, \dots a_{3n}$ because $a_{ij} = a_{ji}$ due to the symmetry).

If we integrate this then we can bring the integral inside the sum and express integrals as Gamma functions $\int_0^\infty x_i^k e^{-x_i^2} dx = \frac{\Gamma((k+1)/2) }{2}$

$$\begin{array}{} \int_{\mathbf{x} \in \mathbb{R}^n_{\geq 0}}\exp \left(-\frac12 \mathbf{x}^T \mathbf{A} \mathbf{x}\right) d\mathbf{x} &=& \int_{\mathbf{x} \in \mathbb{R}^n_{\geq 0}} \sum_{\mathbf{a} \in N^{{n}\choose{2}}} \left[ \frac{(-2)^{\sum_{i<j} a_{ij}}}{\prod_{i<j} a_{ij}!} \prod_{l=1}^n x_{l}^{\sum_{m \neq l} a_{lm}} \prod_{i} e^{-x_{i}^2} \right] \boldsymbol{\alpha}^{\mathbf{a}} d\mathbf{x} \\ &=& \sum_{\mathbf{a} \in N^{{n}\choose{2}}} \left[ \frac{(-2)^{\sum_{i<j} a_{ij}}}{\prod_{i<j} a_{ij}!} \prod_{i} \int_{x_i \in \mathbb{R}_{\geq 0}} x_{i}^{\sum_{m \neq l} a_{lm}} e^{-x_{i}^2} dx \right] \boldsymbol{\alpha}^{\mathbf{a}}\\ &=& \sum_{\mathbf{a} \in N^{{n}\choose{2}}} \left[ \frac{(-2)^{\sum_{i<j} a_{ij}}}{\prod_{i<j} a_{ij}!} \prod_{i} \Gamma\left( \frac{1+\sum_{m \neq l} a_{lm}}{2} \right) \right] \boldsymbol{\alpha}^{\mathbf{a}}\\ \end{array}$$

The R-code below demonstrates this approach and compares it with a Monte Carlo approach to estimate the value. The Monte Carlo approach considers a multivariate normal distribution which has a density of the form ${\det(2 \pi \boldsymbol{\Sigma})}^{-0.5} \exp \left(-\frac12 \mathbf{x}^T \boldsymbol{\Sigma}^{-1} \mathbf{x}\right)$ .

library(MASS)
set.seed(1)

simulations to compute orthant probability

P_mc = function(sig, n = 10^3) {
  dim = length(sig[1,])
  mu = rep(0,dim)
  X = mvrnorm(n, mu, sig)   ### sample from multivariate normal
  Y = (X > 0)

  return(mean(rowSums(Y) == dim))  ### return the mean number of cases when all X>0
}

taylor series to compute orthant probability

P_comp = function(sig, order = 3) {
  k_t = order + 1
  dim = length(sig[1,])
invsig = solve(sig) ### use inverse of Sig to relate with covariance marix of Gaussian used in P_mc
rescale vectors such that diagonal is equal to 1
this does not change the orthant
f = diag(invsig) %*% t(diag(invsig))
  invsig = invsig / sqrt(f)
create a vector with elements from the matrix with condition on subscripts i<j
alpha = invsig[lower.tri(invsig)]
create a matrix with each row containing the combination of powers for the multivariate taylor series
l = length(alpha)
  a_base = c(1:k_t) - 1
  a = a_base
  for (k in 2:l) {
    a = cbind(rep(1, k_t) %x% a, rep(a_base, each = k_t^(k-1)))
  }
  n_rows = length(a[,1])
compute the Taylor series terms
sum_term = sapply(1:n_rows, FUN = function(j) {
    aj = a[j,]
### making a matrix with the power terms we use this to compute term_i
Maj = matrix(rep(1,dim^2),dim)
Maj[lower.tri(Maj) == 1] = aj
Maj = t(Maj)
Maj[lower.tri(Maj) == 1] = aj 

prod1 = prod(factorial(aj))
term_i = sapply(1:dim, FUN = function(i) {gamma( 0.5 * (sum(Maj[i,-i])+1) )})
prod2 = prod(term_i)
prod3 = prod(alpha^aj)
pow = (-2)^sum(aj)
pow/prod1*prod2*prod3 

})
value = sum(sum_term) * det(invsig)^0.5 / (4*pi)^(dim/2)
return(value)
}
some matrix to try out
set.seed(1)
rho = 0.3
sig = matrix(c(1,rho,rho,rho,
               rho,1,rho,rho,
               rho,rho,1,rho,
               rho,rho,rho,1),4)
P_mc(sig = sig, n  =10^6)
0.140251
P_comp(sig, order = 4)
0.1400075
sig = matrix(c(1,  -0.3, 0.1, 0.2,
              -0.3, 1,   0.2, 0.1,
               0.1, 0.2, 1,   0.4,
               0.2, 0.1, 0.4, 1), 4)
P_mc(sig = sig, n  =10^6)
0.088968
P_comp(sig, order = 4)
0.08863386