I was hoping if someone could show me the proof of exactly why this converges to the Euler–Mascheroni constant.
Asked
Active
Viewed 4,589 times
2
-
1While it certainly calls for proof of convergence, the limit is the definition of the Euler-Mascheroni constant. – hardmath Jul 05 '14 at 22:54
-
As long as $f(x), f'(x), f''(x)$ are never zero for $x \geq 1$ and $f''(x) \rightarrow 0,$ there is a limit of $$ \sum_{j=1}^n f(j) - \int_1^n f(x) dx $$ as $n \rightarrow \infty$ – Will Jagy Jul 05 '14 at 23:00
-
See also: http://math.stackexchange.com/questions/344314/showing-that-lim-n-to-infty-sumn-k-1-frac1k-lnn-0-5772-ldots/344574#344574 – Martin Sleziak Jul 06 '14 at 08:41
3 Answers
2
$\qquad$ 
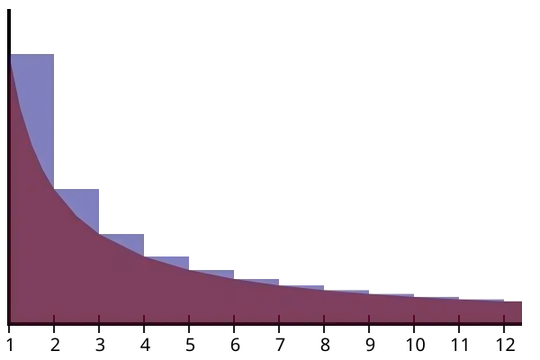
The best thing is to just plot the graphic of both functions, and to interpret it. Notice how the first blue area on the left is smaller than $1-\dfrac12$, the second is smaller than $\dfrac12-\dfrac13$, the third is smaller than $\dfrac13-\dfrac14$, etc. At the same time, all these quantities are positive, meaning that the series is strictly increasing. But it is also bounded by $1$, since $\bigg(1-\dfrac12\bigg)+\bigg(\dfrac12-\dfrac13\bigg)+\bigg(\dfrac13-\dfrac14\bigg)+\ldots$ is telescopic in nature. And since it is both bounded and monotonous, it follows that it converges.
-
The two functions are $f(x)=\dfrac1x$ and $g(x)=\dfrac1{[x]}$ . The area of the former yields the natural logarithm, and that of the latter, the n-th harmonic number. – Lucian Jul 05 '14 at 23:16
1
From the error estimate for the rectangle rule:
$$0 < 1/k - \int_k^{k+1} 1/x dx = \frac{1}{2c_k^2}$$
where $c_k \in (k,k+1)$. So
$$0 < 1/k - \int_k^{k+1} 1/x dx < \frac{1}{2k^2}.$$
Therefore
$$\sum_{k=1}^n 1/k - \ln n = \sum_{k=1}^n 1/k - \int_1^n 1/x dx < \sum_{k=1}^n \frac{1}{2k^2} < \sum_{k=1}^\infty \frac{1}{2k^2} = \frac{\pi^2}{12}.$$
Also, this quantity is increasing, so from the monotone convergence theorem there is a limit. This limit is by definition the Euler-Mascheroni constant, and this argument shows that it is less than $\frac{\pi^2}{12}$. One can repeat the argument, using $c_k < (k+1)$ to get a lower bound of $\sum_{k=2}^\infty \frac{1}{2k^2} = \frac{\pi^2}{12}-\frac{1}{2}.$
Ian
- 101,645
0
The sequence, $$1+\frac{1}{2}+\cdots +\frac{1}{n}- \ln n $$ converges.
Consider the series $$\sum\limits_{n=1}^{\infty} \frac{1}{n}-\ln\left( 1+\frac{1}{n} \right).$$ We show that this series converges. We use the inequality, $$\ln (1+x) < x \qquad \text{for} -1<x <\infty.$$ First, all of its terms are positive, since $$\ln\left( 1+\frac{1}{n} \right) <\frac{1}{n}.$$ We now make a comparison with the telescoping series, $\sum\limits_{n=1}^{\infty} \frac{1}{n(n+1)}$. We have, \begin{equation*} \begin{split} -\ln\left( 1+\frac{1}{n} \right)&=\ln \left( \frac{n}{n+1} \right)\\ &=\ln \left( 1-\frac{1}{n+1} \right)\\ &<-\frac{1}{n+1}\\ \end{split} \end{equation*} So, $$\frac{1}{n}-\ln\left( 1+\frac{1}{n} \right) < \frac{1}{n}-\frac{1}{n+1}=\frac{1}{n(n+1)}.$$ Therefore the series $$\sum\limits_{n=1}^{\infty} \frac{1}{n}-\ln\left( 1+\frac{1}{n} \right)$$ converges.
The $n$th partial sum of this series is $$1+\frac{1}{2}+\cdots +\frac{1}{n}- \ln (n+1) $$ and this differs from our original sequence by a term of $\ln (n+1) -\ln n= \ln\left( 1+\frac{1}{n} \right)$ but this goes to zero as $n$ goes to infinity.
Rene Schipperus
- 39,526