Convergence of $\sum _{k=1}^\infty \sin \left(\sqrt{k}\right)/k$

Question

This was asked at an oral examination.

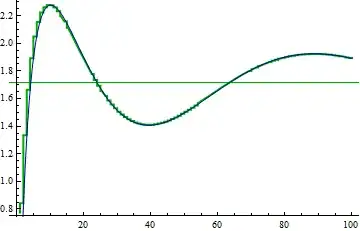
Does the series $\displaystyle \sum _{k\geq1}\frac{\sin\left(\sqrt{k}\right)}{k}$ converge ?

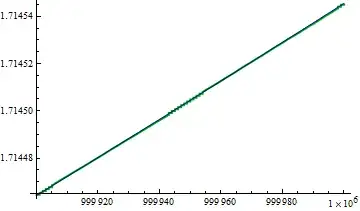
After playing with Mathematica, it's very likely it converges, but slowly (sort of oscillating).

To actually prove convergence, summation by part is useless since $\displaystyle \sum _{k\geq1}\sin\left(\sqrt{k}\right)$ diverges.

Any suggestion is appreciated.

It does converge by the integral test. – Alex Schiff Jun 09 '14 at 19:46 — Alex Schiff, Jun 09 '14 at 19:46
@AlexSchiff, the terms are not nonnegative nonincreasing. – Christopher A. Wong Jun 09 '14 at 19:59 — Christopher A. Wong, Jun 09 '14 at 19:59
Whoopsie daisy, not enough coffee this morning. :-P – Alex Schiff Jun 09 '14 at 20:06 — Alex Schiff, Jun 09 '14 at 20:06

score 16 · Accepted Answer · edited Jun 10 '14 at 13:40

16

The convergence of $\int_1^\infty\frac{\sin\sqrt t}tdt$ can be deduced by a substitution $s=\sqrt t$ and the convergence of $\int_1^\infty\frac{\sin s}sds$. Define $$a_k:=\int_k^{k+1}\frac{\sin\sqrt t}{t}\mathrm dt-\frac{\sin\sqrt k}k$$ and $g(x):=\frac{\sin(\sqrt x)}x$. Since $$g'(x)=\frac{\cos(\sqrt x)}{x^{3/2}}-\frac{\sin(\sqrt x)}{x^2}$$ and by the mean value theorem, $a_k=g'(x_k)$ for some $x_k\in [k,k+1)$, we obtain $$|a_k|\leqslant \frac 2{k^{3/2}},$$ hence $\sum_{k\geqslant 1}|a_k|$ is convergent.

edited Jun 10 '14 at 13:40

answered Jun 09 '14 at 20:00

Davide Giraudo

172,925

There's one thing I don't get: how did you apply the mean value theorem ? – Gabriel Romon Jun 09 '14 at 20:13
Explain why $a_k = g'(x_k)$ by MVT? $a_k$ is not equal to $g(k+1) - g(k)$. – Christopher A. Wong Jun 09 '14 at 20:13
1

@ChristopherA.Wong The integral $\int_k^{k+1}\frac{\sin\sqrt t}{t}\mathrm dt$ is $g(y_k)$ for some $y_k\in [k,k+1]$, then $|g(y_k)-g(k)|\leqslant \sup_{t\in [k,k+1]}|g'(t)|$. – Davide Giraudo Jun 09 '14 at 20:17

martin · Answer 2 · 2014-06-11T06:20:15.290

2

$\sum_{k=1}^{n}\dfrac{\sin(\sqrt{k})}{k}$ plotted against $C-\dfrac{2\cos(\sqrt{k-\sqrt{\pi}})}{\sqrt{k+\sqrt{\pi}}}$, where $C$ is calculated in Mathematica numerically with fact that $\sum_{k=1}^{\infty}\dfrac{\sin(\sqrt{k})}{k}=\sum_{k=1}^{\infty}\dfrac{e^{i\sqrt{k}}}{k}$:

enter image description here

c = Quiet[N[Im[Sum[E^(I Sqrt[k])/k, {k, 1, Infinity}]]]];
Show[Plot[Sum[Sin[Sqrt[k]]/k, {k, 1, n}], {n, 0, 100}, 
GridLines -> {{}, {c}}, GridLinesStyle -> Darker[Green], 
PlotStyle -> {Darker[Green], Thick}], 
Plot[c - 2 Cos[Sqrt[k - Sqrt[Pi]]]/Sqrt[k + Sqrt[Pi]], {k, 0, 100}, 
PlotStyle -> {Darker[Blue], Thin}, PlotRange -> All]]

and for larger $k$:

enter image description here

Quiet[N[Im[Sum[E^(I Sqrt[k])/k, {k, 1, Infinity}]]]]

then gives $C\approx1.7156717726570607\dots$.

edited Jun 11 '14 at 06:20

answered Jun 10 '14 at 13:35

martin

8,998

Thanks for portraying the series. Does WolframAlpha/Mathematica suggests a closed form for the limit ? (Can you copy-paste it with at least 5 digits precision ?) – Gabriel Romon Jun 10 '14 at 13:49
@ G.T.R. - Please see update. – martin Jun 11 '14 at 06:10
Interesting. WolframAlpha finds multiple possible closed Forms for $C$ http://m.wolframalpha.com/input/?i=1.7156717726570607&x=8&y=0 – Gabriel Romon Jun 11 '14 at 08:01
Hmmm ... just typed in completely random number (1.254635278541656) & also came up with possible closed forms ;) – martin Jun 11 '14 at 08:57
Can you get 20 digits precision ? There will be less possible closed Forms then. – Gabriel Romon Jun 11 '14 at 09:25
That is the best Mathematica can do with that sum, I'm afraid! (Hence the Quiet.) – martin Jun 11 '14 at 09:38
On another note, I should imagine that $\sum_{k=1}^{\infty}\dfrac{\sin(k^{1/n})}{k}$ converges for any $n\in\mathbb{N}$. – martin Jun 11 '14 at 10:24

Convergence of $\sum _{k=1}^\infty \sin \left(\sqrt{k}\right)/k$

2 Answers2

Linked

Related