10

Again, inspired by this question, and the great answers I received here, I am curious as to why these infinite sums can be modelled with smooth functions.

It appears that $\sum_{k=1}^{n}\dfrac{\sin(k)}{k}$ can be modelled with $\dfrac{\pi-1}{2}-\dfrac{\cos(k)}{k}$

enter image description here

and that $\sum_{k=1}^{n}\dfrac{\sin(\sqrt{k})}{k}$ can be modelled with $C-\dfrac{2\cos(\sqrt{k})}{\sqrt{k}}$, where $C$ is calculated in Mathematica numerically with fact that $\sum_{k=1}^{\infty}\dfrac{\sin(\sqrt{k})}{k}=\sum_{k=1}^{\infty}\dfrac{e^{i\sqrt{k}}}{k}$:

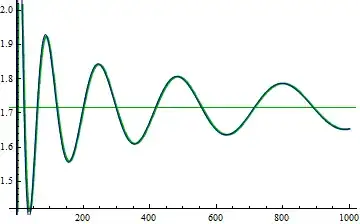
enter image description here

and more generally, that $\sum_{k=1}^{\infty}\dfrac{\sin(k^{1/n})}{k}$ can be modelled with $\dfrac{\pi-1}{2}+j(n-1)-\dfrac{n\cos(k^{1/n})}{k^{1/n}}\text{ for any }n\in\mathbb{N},$ and hence converges to $\dfrac{\pi-1}{2}+j(n-1),\text{ where }j\rightarrow\ \approx 0.6247\dots,$

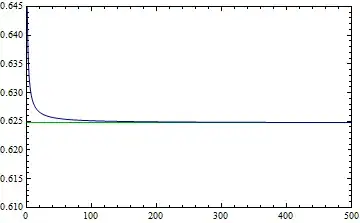
enter image description here

$\sum_{k=1}^{\infty}\dfrac{\sin(k^{1/100})}{k}$ would therefore converge to approximately $\dfrac{\pi-1}{2}+99\times0.62511\dots$

I would very much like to understand this analytically, rather than numerically however.

Update

It appears that $j$ tends to $0.6247\dots$, or $\int_{t=1}^{\infty}\dfrac{\sin(t)}{t}\text{d}t$ (thanks to Yves Daoust's answer below) at a similar rate of convergence as $\dfrac{e-(1-\frac{1}{n})^n}{const}\rightarrow 0$ (where $const\approx35$)

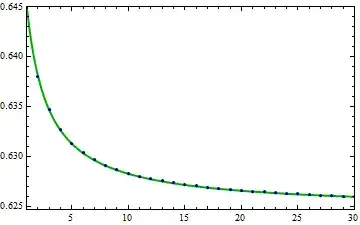
enter image description here

with a relatively small error

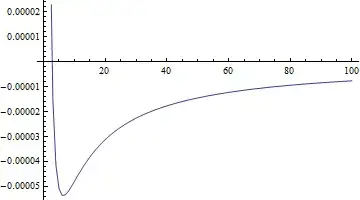
enter image description here

The convergence value of $\sum_{k=1}^{\infty}\dfrac{\sin(k^{1/n})}{k}$ for any positive real $n$ can therefore be approximated by $$\dfrac{\pi-1}{2}+\bigg(\int_{t=1}^{\infty}\dfrac{\sin(t)}{t}\text{d}t+\dfrac{e-(1-\frac{1}{n-1})^{n-1}}{35}\bigg)(n-1)$$ compare (for $n>1$):

n = 10;
p = Quiet[N[Im[Sum[E^(I k^(1/n))/k, {k, 1, Infinity}]]]];
j1 = w /. FindRoot[p - (\[Pi] - 1)/2 == N[w (n - 1)], {w, 1}];
j2 = NIntegrate[Sin[t]/t, {t, 1, Infinity}] + (E-(1 + 1/(n-1))^(n-1))/35;
(\[Pi] - 1)/2 + j1 (n - 1)
(\[Pi] - 1)/2 + j2 (n - 1)

It is not that great for very small $n>1$ though! It would be nice to know the exact rate of convergence to $\int_{t=1}^{\infty}\dfrac{\sin(t)}{t}\text{d}t$

Update 2

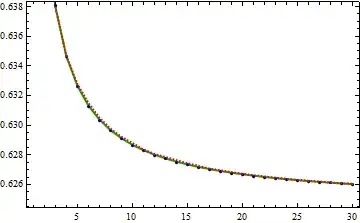
enter image description here

where red line is given by \begin{align*} n \left( \frac{\pi}{2} - \mathrm{Si}(1) \right) + \frac{\sin a}{2} + \int_{1}^{\infty} \frac{ax^{1/n}\cos(ax^{1/n}) - n \sin(ax^{1/n})}{n x^{2}} \tilde{B}_{1}(x) \, dx \end{align*} for $a=1,$ as shown in sos440's answer below.

Examples for $n=2$ and $n=3$:

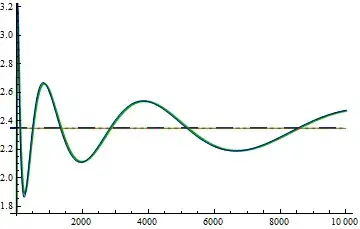
where the discrepancy between the red line and the "actual" is due to numerical error in computation.

Martin Sleziak
  • 53,687
martin
  • 8,998

2 Answers2

2

Here is a more detailed reasoning: Using the Riemann-Stieltjes integral and the periodic Bernoulli polynomials $\tilde{B}_{n}(x)$, for $a > 0$

\begin{align*} \sum_{k=1}^{N} \frac{\sin(k^{1/n}a)}{k} &= \int_{1-}^{N} \frac{\sin(x^{1/n}a)}{x} \, d[x] \\ &= \int_{1}^{N} \frac{\sin(x^{1/n}a)}{x} \, dx - \int_{1-}^{N} \frac{\sin(x^{1/n}a)}{x} \, d\tilde{B}_{1}(x) \\ &= n \int_{1}^{a N^{1/n}} \frac{\sin x}{x} \, dx - \int_{1-}^{N^{1/n}} \frac{\sin(ax)}{x^{n}} \, d\tilde{B}_{1}(x^{n}). \end{align*}

So let us focus on the second term. Integrating by parts,

\begin{align*} - \int_{1-}^{N^{1/n}} \frac{\sin(ax)}{x^{n}} \, d\tilde{B}_{1}(x^{n}) &= \left[ -\frac{\sin(ax)}{x^{n}} \tilde{B}_{1}(x^{n}) \right]_{1-}^{N^{1/n}} + \int_{1}^{N^{1/n}} \left( \frac{\sin(ax)}{x^{n}} \right)' \tilde{B}_{1}(x^{n}) \, dx \\ &= \frac{\sin a}{2} + \int_{1}^{\infty} \frac{ax^{1/n}\cos(ax^{1/n}) - n \sin(ax^{1/n})}{n x^{2}} \tilde{B}_{1}(x) \, dx \\ &\qquad + \mathcal{O}(N^{-1+1/n}). \end{align*}

(But in fact, due the cancelling behavior, the error estimate may be improved further.) So when $n > 1$, combining together gives

$$ \sum_{k=1}^{N} \frac{\sin(a k^{1/n})}{k} = C + \mathcal{O}(\max \{ N^{-1+1/n}, N^{-1/n} \} ), $$

where

\begin{align*} C &= \sum_{k=1}^{\infty} \frac{\sin(a k^{1/n})}{k} \\ &= n \left( \frac{\pi}{2} - \mathrm{Si}(1) \right) + \frac{\sin a}{2} + \int_{1}^{\infty} \frac{ax^{1/n}\cos(ax^{1/n}) - n \sin(ax^{1/n})}{n x^{2}} \tilde{B}_{1}(x) \, dx. \end{align*}

And I highly suspect that the ever-growing error results from computation errors, not from the actual difference between the sum and the $N$-th partial sum.

Added. If you execute the following code,

  a = 1;
  n = 2;
  Quiet[N[Im[Sum[E^(I k^(1/n))/k, {k, 1, Infinity}]]]]
  Quiet[N[n (Pi/2 - SinIntegral[1]) + Sin[a]/2 + NIntegrate[(BernoulliB[1, FractionalPart[x]] (a x^(1/n) Cos[a x^(1/n)] - n Sin[a x^(1/n)]))/(n x^2), {x, 1, Infinity}]]]
  Quiet[N[n (Pi/2 - SinIntegral[1]) + Sin[a]/2 + NIntegrate[(BernoulliB[1, FractionalPart[x]] (a x^(1/n) Cos[a x^(1/n)] - n Sin[a x^(1/n)]))/(n x^2), {x, 1, Infinity}, WorkingPrecision -> 200, PrecisionGoal -> 50]]]
  Quiet[N[n (Pi/2 - SinIntegral[1]) + Sin[a]/2 + NIntegrate[(BernoulliB[1, FractionalPart[x]] (a x^(1/n) Cos[a x^(1/n)] - n Sin[a x^(1/n)]))/(n x^2), {x, 1, Infinity}, WorkingPrecision -> 400, PrecisionGoal -> 50]]]
  Quiet[N[n (Pi/2 - SinIntegral[1]) + Sin[a]/2 + NIntegrate[(BernoulliB[1, FractionalPart[x]] (a x^(1/n) Cos[a x^(1/n)] - n Sin[a x^(1/n)]))/(n x^2), {x, 1, Infinity}, WorkingPrecision -> 600, PrecisionGoal -> 50]]]
  Clear[a, n];

Then you will see how the numerical methods used in Mathematica are susceptible:

  1.71567
  1.72229
  1.71513
  1.71661
  1.71436
Sangchul Lee
  • 167,468
1

Consider the integral $$\int_1^k\frac{\sin x^{1/n}}xdx=n\int_1^{k^{1/n}}\frac{\sin t}t\ dt$$ by the change of variable $x=t^n$.

This is the Sine Integral.

It is closely related to your sum, and explains why the value of the exponent $n$ doesn't have such a big impact on the behavior.