I am regular user of StackOverflow, but new here.
I'm trying to guess how to do that:
Given a straight line (x1, y1, x2, y2) how can i get the point into the line (x, y) who are at an n distance from x1, y1?
I'm very bad with math, and I'm developing a 2D game. That should be forbidden!!
Thank you very much!!
Let us try from an algebraic point of view. Your three points are along a straight line defined by two points $(x_1,y_1)$ and $(x_2,y_2)$. So, let write the equation as $y = a +b x$ and create the two equations in order to find $a$ and $b$. So, we have $$ y_1=a+b x_1$$ $$ y_2=a+b x_2$$ from there $$a=\frac {x_1 y_2-x_2 y_1}{x_1-x_2}$$ $$b=\frac {y_1-y_2}{x_1-x_2}$$ Now the new point $(x,y)$ is along the line which means that $$y=a+b x$$ and the squared distance from point $(x_1,y_1)$ is given by $$(x-x_1)^2+(y-y_1)^2=n^2$$ In this last expression, everything is know beside $x$ which can be extracted and since you need $x \gt x_1$, the solution is then given by $$x=x_1+\frac{n^2 ({x_1}-{x_2})^2}{\sqrt{n^2 ({x_1}-{x_2})^2 \left(({x_1}-{x_2})^2+({y_1}-{y_2})^2\right)}}=x_1+\frac{n ({x_2}-{x_1})}{\sqrt{ \left(({x_1}-{x_2})^2+({y_1}-{y_2})^2\right)}}$$ and $$y=\frac {x_1 y_2-x_2 y_1}{x_1-x_2}+\frac {y_1-y_2}{x_1-x_2} x$$
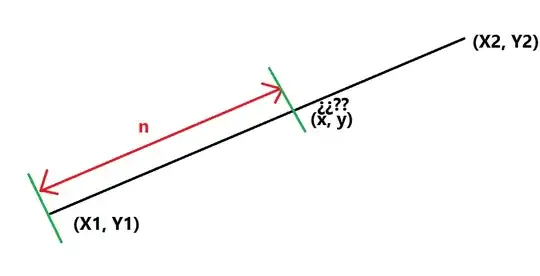
The same question is asked and answered here -- Move Point A along a line -- but with slightly different notation. Let's adapt one of its solutions to your $x$-$y$ coordinates.
The length of your original line segment from $(x_1,y_1)$ to $(x_2,y_2)$ is
\begin{equation} L = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}. \end{equation}
So if you happened to want the distance from $(x_1,y_1)$ to $(x,y)$ to be $L$, the answer would be trivial. But you want to move a different distance from $(x_1,y_1)$; specifically, you want the distance to be $n/L$ times as far. So we find $(x,y)$ this way:
\begin{equation} x = x_1 + \frac{n}{L}(x_2 - x_1), \end{equation}
\begin{equation} y = y_1 + \frac{n}{L}(y_2 - y_1). \end{equation}
So you just have to use these formulas to compute $L$ and then compute $x$ and $y$.
A word on how this works: In the case where $n = L$, this would add just enough to $x_1$ and $y_1$ so that you would reach $(x_2,y_2)$, but if $n < L$ it moves you to a point not so far from $(x_1,y_1)$, and if $n > L$ it moves you to a farther point, beyond $(x_2,y_2)$.
