5

Sorry, can't post images if my rep is below 10, and can't post more than 2 links. I removed the http section so it won't count as a link. I hope this isn't against forum rules, I'm not hurting anyone.

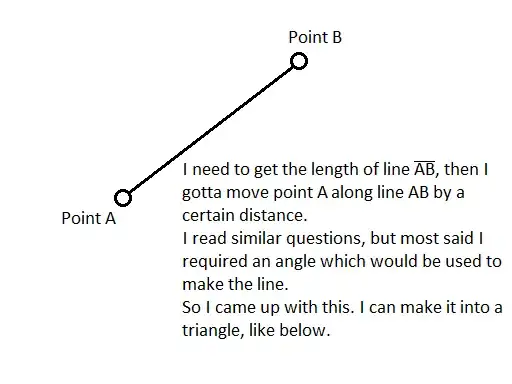
i.stack.imgur.com/6nTKo.png

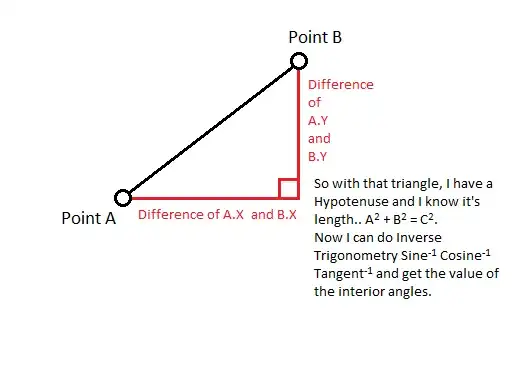
i.stack.imgur.com/Fkbgt.png

i.stack.imgur.com/IHVhL.png

I checked other questions, like this one (A line moving along the hypotenuse of a right triangle) but the answer was too complicated for me to understand. If someone can explain it again, can you please do it in simpler terms?

Community
  • 1
Dave
  • 219

1 Answers1

3

Assuming that $C$ is the origin, try $P = d\cdot(\cos(\angle A),\sin(\angle A)) + (A-C)$ where $d$ is the length you need to move your point from point $A$, or try $P = (-d')\cdot(\cos(\angle A),\sin(\angle A)) + (B-C)$ where $d'$ is the length from point $B$.

In fact you could have skipped the trigonometry thing, just set $k = \frac{d}{\mathrm{Length}(AB)}$ or $k' = \frac{d'}{\mathrm{Length}(AB)}$ and calculate $$P = k\cdot B + (1-k)\cdot A$$ or $$P = k'\cdot A + (1-k')\cdot B.$$

I hope this helps ;-)

dtldarek
  • 37,381
  • I'm sorry, I'm not too good with math. B - C is getting the difference of the points? And the comma between cosA and sinA, what is that? I'm guessing cosA is like X and sinA is like Y and you add it to the difference of the points B and C? I have no idea what the upside down Y is. Is this college level geometry? – Dave Jul 05 '13 at 14:04
  • @user2544245 It's just a different notation. If $P.x = 5 $and $P.y = 123$, then I write $P = (5,123)$. Simirarly $(\cos \alpha, \sin \alpha)$ is just some point (without a name) of coordinates $x = \cos\alpha$ and $y = \sin\alpha$, finally $d\cdot(x,y) = (d\cdot x, d\cdot y)$. – dtldarek Jul 05 '13 at 14:08
  • Hmm, so If I change the origin, I only have to the value of C? – Dave Jul 05 '13 at 14:13
  • $\lambda$ is the Greek letter lambda, it's 'l', like $\alpha$ is 'a' and $\beta$ is 'b'; it does not mean anything in particular. I suggest the second approach, then you can have your origin anywhere you want (and no angle calculations). – dtldarek Jul 05 '13 at 14:15
  • Following the second formula, to get lambda, I need to divide distance by absolute value of point A times point B. Point A times Point B would return (0,0), since each have 0 for one dimension. – Dave Jul 05 '13 at 14:19
  • $|AB|$ was meant to denote the length of $AB$. – dtldarek Jul 05 '13 at 14:24
  • Yup, I have no idea what that means. Is there anyway to explain this is high-school level? – Dave Jul 05 '13 at 14:26
  • It is school level, I'm just bad at explaining. Is it more understandable now? – dtldarek Jul 05 '13 at 14:27
  • Maybe I'm overthinking this? Can't I just treat the Hypotenuse like a normal flat line? If it were flat, then I could easily add an X value to the starting point. From my angle, it seems diagonal, but in reality it's flat if I rotate my head. So isn't there an easier way? This is what I mean. The length of the Hypotenuse is 10, and I want to move point a 4 along the line. Can't I just add up point A and B, and multiply it by .4? – Dave Jul 05 '13 at 14:28
  • Ok, let me put it another way, do you know that $M = \frac{A+B}{2}$ (yeah, exactly like the arithmetic mean) is the middle point of segment $AB$? – dtldarek Jul 05 '13 at 14:35
  • Yup. Let's assume A is at (0,6) and B is at (8,0). So if I want to move point A along line AB by 2.5 units (length of AB is 10) I do A+B = (8,6) * (2.5/10) = (2, 1.5). The X value seems correct. But the Y value is off. The Y value would be correct if I was moving Point B. So to correct the Y value, I just get the 'other side' of the Y? 6 - 1.5 = 4.5. So: Point A after moving it along line AB by 2.5 distance becomes (2, 4.5)? – Dave Jul 05 '13 at 14:40
  • First you have $k = 2.5/10 = 1/4$. Now, you should do $P = kB+(1-k)A = 1/4(8,0) + 3/4(0,6) = (2,0) + (0,4.5) = (2,4.5)$. – dtldarek Jul 05 '13 at 14:47
  • Also, points $N_1 = \frac{A+A+B}{3}$ and $N_2 = \frac{A+B+B}{3}$ split segment $AB$ into three equal parts. In fact $\frac{pA+qB}{p+q}$ splits $AB$ in ratio $p:q$. All that is left is to calculate the ratio you want to use, that is $\frac{d}{\mathrm{Length}(AB)}$. – dtldarek Jul 05 '13 at 14:53
  • Alright, thanks for everything. I got what I needed. – Dave Jul 05 '13 at 15:21