1

$\bf\sf37.$ Evaluate $\iiint_E z\,dV,$ where $E$ lies above the paraboloid $z=x^2+y^2$ and below the plane $z=2y.$

In cylindrical coordinates the paraboloid is given by $z=r^2$ and the plane by $z=2r\sin\theta$ and they intersect in the circle $r=2\sin\theta$. Then $\iiint_E z\,dV=\int_0^\pi\int_0^{2r\sin\theta}rz\,dz\,dr\,d\theta=\tfrac{5\pi}6.$ [using a CAS]

The solution claims that the domain of integration $= \{ \, 0 \le \theta \le \color{red}{ \pi }, 0 \le r \le 2\sin\theta, r^2 \le z \le 2r \sin\theta \, \} $. Why isn’t the upper bound on $\theta$: $\color{red}{ 2 \pi } $?

$1.$ I know $ x^2 + y^2 = 2y \iff r = 2\sin\theta$. But how does this become the upper bound on $r$?

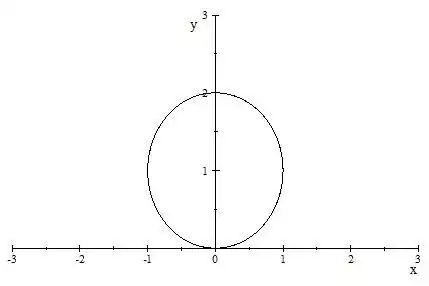
$2.$ Conforming to the solution, the projection (onto $z=0$) of the intersection of paraboloid and plane $= x^2 + y^2 = 2y \iff x^2 + (y - 1)^2 = 1$, a circle of radius 1 centered at $(0, 1)$.
Aren’t we concerned with this entire circle?

I tried to plot this: https://mathematica.stackexchange.com/q/45059/9983

Community
  • 1

2 Answers2

1
  1. The projection is a circle as you indicated.
  2. The circle passing through the origin.
  3. The circle has center at $\color{red}{(0,1)}$ not $(0,0.5)$ and it has radius $\color{red}{1}$

So, the circle lies in the upper half of the xy-plane where $y\ge 0$.

  1. The radial arm ranges from o to 1
  2. The radial arm starts at $\theta=0$ on the positive x axis
  3. The radial arm covers the disk at $\theta=\pi$ on the negative x axis.

The following figures represent the projection on xy-plane

Hakim
  • 10,213
Semsem
  • 7,651
  • Regrettably, I don't perceive your answer. Would you please elucidate in your answer (not as a comment)? –  Apr 04 '14 at 06:58
  • +1. Thank you effusively for your continual care! To confirm, are you saying that $0 \le \theta$ because this circle lies in the upper half of the $xy-$ plane? –  Apr 11 '14 at 15:21
  • Would you please respond in your answer (and not as a comment)? –  Apr 11 '14 at 15:27
0

Okay, so the first thing to take into account, is that the intersection is a circle, but it is not parallel with the $xy$ plane, it is instead at an angle, which is what leads to what I would call an unorthodox parametrisation.

If we consider $\{0\le\theta\le\pi,0\le r\le 2\sin\theta\}$, this parametrises a circle, (it is actually the circle presented in Semsem's answer), I have entered if here in wolfram: https://www.wolframalpha.com/input/?i=plot+r%3D2sin%28x%29+for+x+from+0+to+pi

The reason that $2\sin\theta$ is the upperbound, is that it represents the length of the line from the origin $(0,0)$ to the point $(\theta,r)$, (when you consider the image in my link), (in my link just think of $x$ as $\theta$).

So all in all this answers $(1)$ and $(2)$, its just not the standard way of parameterising a circle.

the maximum value for $\theta$ is $\pi$ because $0\le\theta\le\pi$, is all that is needed to produce the circle, if you had $0\le\theta\le 2\pi$, this would go round the circle twice.

Ellya
  • 11,783
  • +1. Thanks. And why is $pi$ the upper bound on $\theta$? –  Jun 01 '14 at 19:46
  • see my edit :), by the way was my answer for http://math.stackexchange.com/questions/614083/proof-strategy-tricky-question-involving-distinct-non-zero-eigenvalues-of-a/812287#812287 sufficient? – Ellya Jun 01 '14 at 19:49
  • Thank you. Yes. I'll return in a few days. –  Jun 02 '14 at 15:05
  • Okie doke, would hate to see that bounty go :) – Ellya Jun 02 '14 at 15:11