With Stokes's Theorem - Calculate $\iint_S \operatorname{curl} \mathbf{F} \cdot\; d\mathbf{S}$ for $\mathbf{F} = (-y^3,x^3,z^3)$

Question

2012 9C. Consider the (cutoff) paraboloid defined by $z=x^2 + y^2, \frac{1}{9} \le z \le 1$. Sketch the surface. Verify Stokes’s Theorem for for $\mathbf{F} = (-y^3,x^3,z^3)$.

Herein, I ask only about computing line integrals instead of $ \iint_S (\nabla × F )· d\mathbf{S}$, by virtue of Stokes's Theorem. I think there are two boundary curves: $x^2 + y^2 = z \; = 1$ and $x^2 + y^2 = z \; = 1/9$.
♦ denote objects that don't need to be computed because they're dot-producted with 0.

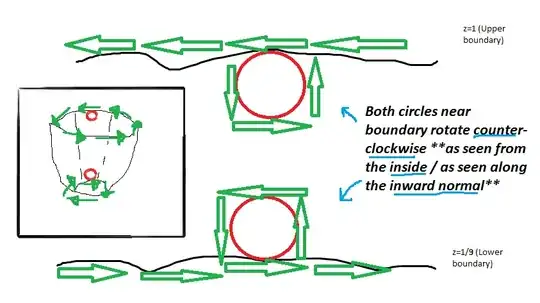
$\bbox[5px,border:2px solid gray]{ \text{ z = 1 cross-section } }$ By virtue of the quotes on orientation here, we need the normal vector to be upward, in the direction of $(0, 0, 1).$ So the circle must be oriented anticlockwise when viewed from above $z = 1$ (as in my picture here). Thus, parameterise with $\mathbf{r}(t) = ( 1\cos t, 1\sin t, 1 )$ for all $0 \le t \le 2\pi$.

Then $\oint_{z = 1 \, curve} \mathbf{F} \cdot d\mathbf{r} = \int^{2\pi}_{0} (-\sin^3 (t) , \cos^3(t), ♦) \cdot ( -\sin t, \cos t , 0) \, dt $ = ... = $3\pi/2.$

$\bbox[5px,border:2px solid gray]{ \text{ z = 1/9 cross-section } }$ By virtue of the quotes on orientation here, we need the normal vector to be downward, in the direction of $(0, 0, -1).$ So the circle must be oriented anticlockwise when viewed from BELOW $z = 1/9$ $\iff$ the circle must be oriented clockwise when viewed from ABOVE $z = 1/9$ (as in my picture here). Thus, parameterise with $\mathbf{r}(t) = ( 1 \sin t, 1\cos t, 1/9 )$ for all $0 \le t \le 2\pi$.

This last line is wrong. I did forget the radius = $1/3$. It's supposed to be $\mathbf{r}(t) = ( \color{red} {1/3} \sin t, \color{red} {1/3} \cos t, 1/9 )$ for all $0 \le t \le 2\pi$.

Then $\oint_{z = 1/9 \, curve} \mathbf{F} \cdot d\mathbf{r} = \int^{2\pi}_{0} ( \color{red}{ \dfrac{-1}{27} } \cos^3 (t) , \color{red}{ \dfrac{1}{27} } \sin^3(t), ♦) \cdot ( \color{red}{ \dfrac{1}{3} } \cos t, \color{red}{ \dfrac{-1}{3} } \sin t , 0) \, dt \\ = - \color{red}{ \dfrac{-1}{81} } \oint_{z = 1 \, curve} \mathbf{F} \cdot d\mathbf{r}. $

In toto, $ \iint_S (\nabla × F )· d\mathbf{S} = \oint_{z = 1 \, curve} \mathbf{F} \cdot d\mathbf{r} + \oint_{z = 1/9 \, curve} \mathbf{F} \cdot d\mathbf{r} = 3\pi/2(1 - \color{red}{ \dfrac{1}{81} }) = \pi40/27$.

Answer 1

From other post

On the other hand, Stokes' Theorem tells us that this can be written as the line integral of $\mathbf{F}$ over the boundary of $S$, which is the two circles $(1/3\cos t,1/3\sin t,1/9)$ and $(\cos t,\sin t,1)$ at the bottom and top of the region.

"Since I have oriented the region inwards"? Would you please explain where you did this? I didn't choose to orient the surface; I just assumed the positive (outward) orientation because my book told me to: Which Cross Product for the Desired Orientation of a Sphere ? [Stewart P1091 16.7.23]

• As I wrote in the other post, I didn't know that the problem specified a normal direction, so I just chose the inward normal arbitrarily. Since it apparently called for the other normal, you would have to multiply that normal by $-1$ to get its outward counterpart.
• (see other post for this too) If you imaging the normal vector that I picked - $(-2x,-2y,1)$ - you will see that it points up, and into the inside of the paraboloid. This is why I say I oriented the region "inwards". The outward normal would have to point down. Note that this normal points up everywhere, even at the bottom.

Since I have oriented the region inwards, the top circle should be anti-clockwise and the bottom circle clockwise.

From which direction are you viewing the circles? Does my writing on how I chose the direction describe what you mean 100%?

• It looks pretty close. You have to imagine looking along the normal vector (from inside the paraboloid in this case) and seeing what a counterclockwise rotation would cause the boundary curve to do. Consult this picture - I apologize in advance for this :)

Looking from the inside (you would have to look from the outside if you used the outward normal), we see that counterclockwise rotation over the surface would cause the upper boundary to go counterclockwise and the bottom boundary to go clockwise.

Hence we find $$\int_{\partial S}\mathbf{F}\cdot \mathrm{d}\mathbf{s}=-\int_0^{2\pi}(-1/27\sin^3 t,1/27\cos^3 t,1/9^3)\cdot (-1/3\sin t,1/3\cos t,0)\,\mathrm{d}t+\int_0^{2\pi}(-\sin^3 t,\cos^3 t,1)\cdot (-\sin t,\cos t,0)\,\mathrm{d}t$$ $$=\left(-{1\over 81}+1\right)\int_0^{2\pi}\sin^4 t+\cos^4 t\,\mathrm{d}t=\frac{80}{81}\cdot\frac{3\pi}{2}=\frac{40\pi}{27}$$ and the answers do indeed agree. I used Wolfram Alpha for that last integral, you could solve it by hand using double-angle formulas and the identity $\int_0^{2\pi}\cos^2 x\,\mathrm{d}x=\int_0^{2\pi}\sin^2 x\,\mathrm{d}x=\pi$.

Also note that the $z$-components of the line integrals went to zero. This is because the field can be written as $$\mathbf{F}=(-y^3,x^3,0)+(0,0,z^3)=(-y^3,x^3,0)+\nabla(z^4/4)$$ where the second part is conservative, and hence zero over closed curves. Sorry I don't know how to make the contour integral sign with $\LaTeX$ but note that the boundary of a region used in Stokes' Theorem is always closed, so the same sort of simplification (you could just consider the first part and disregard the second part of the field) is always possible if you can break $\mathbf{F}$ into pieces, some of which are conservative.

---

Answers to Questions

What do the red circles mean in your picture?

The red circles should have counter-clockwise rotations on them. They represent the counter-clockwise rotation that is happening everywhere on the surface of the paraboloid. You can see where the circles "touch" the boundary curves, and how they induce an orientation for those curves.

Also, what point of view is the picture NOT in the black box showing?

The black box shows the whole paraboloid. The other part shows a zoomed-in representation, where you can see in detail how the counter-clockwise red rotations induce rotations along the boundary curves. In this case, the top curve ends up being counter-clockwise and the bottom curve clockwise (as viewed from above). It is the same view, just closer to the object (think of going through the surface nearest you in the black box picture).

To confirm, the inward normal $=(−2x,−2y,1)$ always points up, just because the $z$-component $=1>0$, regardless of $x,y$?

That is correct.