Which Cross Product for the Desired Orientation of a Sphere ? [Stewart P1091 16.7.23]

Question

P1086: For a closed surface, the positive orientation is the one for which the normal vectors point outward from the surface, and inward-pointing normals give the negative orientation.

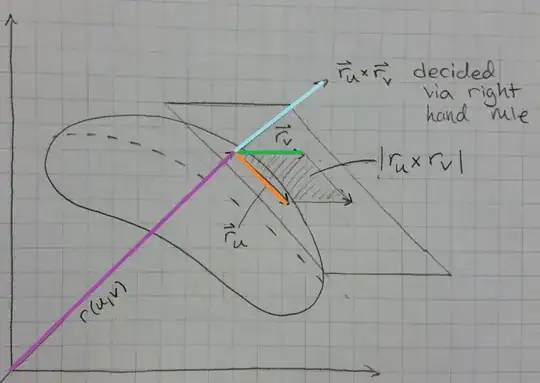
P1087: If $S$ is a smooth orientable surface given in parametric form by a vector function $\mathbf{r}(u,v)$, then it is automatically supplied with the orientation of the unit normal $\mathbf{n} = \cfrac{\partial_u\mathbf{r} \times \partial_v\mathbf{r}}{\vert \partial_u\mathbf{r} \times \partial_v \mathbf{r} \vert} $...

P1093: The orientation of a surface S induces the positive orientation of the boundary curve C shown in the figure. This means that if one walks in the positive direction around the curve with one's head pointing in the direction of $\mathbf{n}$, then the surface is always on one's left.

How does one determine whether $\partial_{\huge{u}}\mathbf{r} \times \partial_{\huge{v}}\mathbf{r} \quad \text{ or } \quad \partial_{\huge{v}}\mathbf{r} \times \partial_{\huge{u}}\mathbf{r} \quad $ (negatives of each other) matches the desired orientation?

Since a surface may be hard to sketch (especially under exam conditions), I was hoping for an argument that isn't geometric or visual. But if geometry and visualisation are the easiest, would you please provide pictures for your explanations?

---

P1091 16.7.$23 \text{ generalised.}$ $\mathbf{F} = (x,-z,y)$ and $S$ is the part of $x^2 + y^2 + z^2 = p$ in the first octant and oriented towards $(0,0,0)$. Evaluate the surface integral $\iint_S \mathbf{F} \cdot d\mathbf{S}$. For closed surfaces, use the positive (outward) orientation.

Solution: Since $S$ is a sphere, parameterize with $r(\theta, \phi) = (p\sin \theta \cos \theta, p \sin \theta \sin \theta, p \cos \phi)$.
Then $\mathbf{F[r(\theta, \phi)]} \cdot \color{red}{(\partial_{\theta} r \times \ \partial_{\phi} r )} = p^3 \sin^3 \theta \cos^2 \theta \qquad (♦)$
Then $\iint_S \mathbf{F} \cdot d\mathbf{S} = \iint_D \mathbf{F} \cdot (\partial_{\theta} r \times \ \partial_{\phi} r ) \, dA = p^3\int^{2\pi}_0 \cos^2 \theta \, d\theta \int^{\pi/2}_9 \sin^3 \phi \, d\phi = ... = p^3 \quad \pi \quad 1/3.$ The answer is given as $ -p^\color{red}{2} \quad \pi \quad 1/3 $.

How would've one determined that the cross product in (♦) coloured in red is wrong,
and that it should've been $\color{green}{ \partial_{\large{\phi}} r \times \partial_{\large{\theta}} r }$ ?

Predicated on user Dan's Answer:

Answer 1

There's no fixed answer to this, because whichever one you choose, if you were to reverse $u$ and $v$, you would have to choose the other one. It depends on how the $u$ and $v$ coordinates are oriented on the surface.

However, "$\color{brown}{\text{if the positive $u$ and $v$ tangent vectors at a point are oriented such that,}}$ when looking from the outside of the surface at the point, $\color{brown}{\text{the direction from $u$ to $v$ is counterclockwise, then $\partial u \times \partial v$ is the correct choice.}}$"

Answer 2

A surface $S$ as such is a "two-dimensional smooth set of points" embedded in three-space. At each point $p\in S$ we have a tangent plane $T_p(\sim{\mathbb R}^2)$ with origin at $p$, and this tangent plane has a well defined orthogonal complement $N:=T_p^\perp$, a line through $p$ with origin at $p$. On this line one can measure lengths, but a-priori it does not have a positive, let alone: correct, sense of direction.

For certain purposes, in particular when it comes to the computation of flows, one would like to single out one of the two possible senses as positive, and this in a manner depending continuously on $p$. This can be done in various ways, either by words like "outward", "inward", "upward", "to the right" referring to the implied $(x,y,z)$-coordinate system, or by saying that for a certain parametrization $(u,v)\mapsto{\bf r}(u,v)$ the orientation induced by ${\bf r}_u\times{\bf r}_v$ (in this order!) is positive. Such an explicit directive has to be given by the person that hands you the surface and tells you to do something with it; it does not come out of thin air.

When you are given a geometric description of $S$ (e.g., "the piece of an ellipsoidal surface with axes $\ldots$ bounded by $\ldots$" ), together with the intended orientation, and you look up a parametric representation of $S$ in a catalogue then you have to verify using geometric vizualization (even in an exam situation) whether ${\bf r}_u\times{\bf r}_v$ induces the intended orientation or not.

Answer 3

Answer one: If you make the wrong choice, you get minus the correct answer. If you make the correct choice, you get the correct answer. It is trivial to correct a posteriori and computationally intractable to correct a priori. As an example: what is the correct choice on the surface of the Klein bottle. (This is a cheat since this surface is composed of two Moebius strips. Moebius strips are nonorientable -- there is no consistent choice of surface normal.)

Answer two: A technique, that is entirely computational and also infeasible during an exam, is this: Extend the surface normal from the point on the surface to the point at infinity. Compute the number of times this ray subsequently intersects the surface (at other places). If that number is even, then the normal points outward; if odd, inward. (Caveat: If the ray is tangent to the surface at some point, perturb the angle infinitesimally so that it is no longer tangent.)

Note that this technique informs that both choices of surface normal at each point on a Moebius strip are outward pointing (except for a small segment near the twist where the ray passes through the "opposite arc" of the Moebius strip -- which segment is apparently inwardly pointing while still being smoothly attached to outwardly pointing points under a smooth continuation of chioce of normal.)

Answer three: You must develop intuition for the objects with which you work. If you are working with surfaces in $\mathbb{R}^3$, you must understand these surfaces more thoroughly than as just a bunch of symbols on paper.

Answer 4

Well there is a definite answer for each example here, but as Ted mentions its definitely up to the situation in general. All these problems likely fall under the blanket statement that the positive normal vector is the outward pointing one to the surface ( a usual choice). I find the best way to determine direction is to imagine a small triplet of axes that define the coordinate system at hand on the surface.

For example, the sphere, draw an arbitrary position vector from the origin to the surface of the sphere. At the tip of the position vector draw the two tangent vectors $\partial_{\Large{\phi}} \mathbf{r}$ and $\partial_{\Large{\theta}} \mathbf{r}$, they are tangent to the surface and point in the direction of the rate of change of r with respect to the two angular coordinates.

Say our position vector lies in the first octant. Which direction does $\partial_{\Large{\phi}} \mathbf{r}$ point in? Well $\phi$ is defined as the angle starting from positive z and extending down to negative z, thus $\partial_{\Large{\phi}} \mathbf{r}$ (the phi tangent vector) will always point so as to go down the outside of the sphere. $\color{red} { \text { Would you please explain the previous sentence with your picture? } }$ The theta tangent vector points in the direction of increasing theta, that is around the sphere from positive x axis all the way around back to the x axis in a CCW direction as seen from above. $\color{red} { \text { Would you please explain the previous sentence with your picture? } }$ So we can visualise what the two vectors look like and we merely need to use the right hand rule for cross products to determine the order of the cross product so as to gain the positive outward normal, in this case $\partial_{\phi} r \times \partial_{\theta} r$

http://tinypic.com/r/33xd0lu/8

This image explains both $r_{\theta} \text{ and } r_{\phi}$, these vectors are defined in the sense of the original definition of spherical coordinates, that is the definition of $r_{\theta}$ is the vector wherein all but the theta variable are held constant and the vector is varied in the theta direction. This is why the $\phi$ derivative of r points downward, and the $\theta$ derivative of r points around the outside of the circle.

We can form similar rules for each additional example, draw in an arbitrary position vector r(u,v), then draw in to the best of your ability the two tangent vectors, and using the right hand rule match the order of the vectors so as to supply the outward directed normal.