2

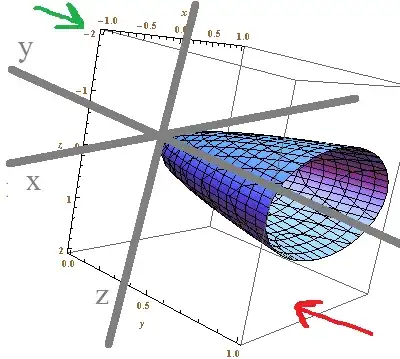
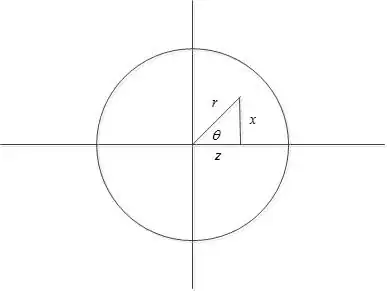
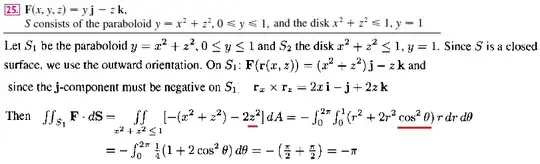enter image description here

$1.$ The unit disk is projected onto the xz-plane, so shouldn’t $x = 1\cos \theta$ and $\color{red}{z = 1 \sin \theta} $?

User Semsem below kindly identified the problem: The normal to the disk is on the direction $-j$ so we have to reverse the orientation as follows.

$2.$ Would someone please explain why the orientation must be reversed? By "reverse", does Semsem mean the following, that thee $xz$-plane should be viewed in the direction of the green arrow (instead in that of the red arrow, which was my problem)?

enter image description here

Community
  • 1
  • Actually orientation doesn't matter at all in this step, since you had to take care of it already in going from $\mathbf F\cdot d\mathbf S$ to $g(x,z),dA$. Now you're just picking a polar-coordinate parametrization of the $xz$-plane, and it doesn't matter if you pick $x=r\cos\theta, z=r\sin\theta$, or $x=r\sin\theta, z=r\cos\theta$, or even $x=-r\sin\theta, z=-r\cos\theta$, anything of that sort. If you're really worried about orientation for whatever reason, you can pick $x=r\cos(\theta+\pi/2), z=r\sin(\theta+\pi/2)$ which still leads to Stewart's result. –  Apr 23 '14 at 05:13
  • @Rahul: Why doesn't it matter that I had picked $x = r\cos\theta, z = r\sin\theta$? The choice of $z$ in my work changes the integrand and thus possibly the final value? –  Apr 23 '14 at 09:25
  • It's just a choice of coordinate transformation, i.e. a change of variables, so it can't change the final value. The integrand changes but so do the limits of integration, and it all works out in the end. Of course, in this case, you're integrating over a disk, so what happens to the limits I leave to you to figure out... :) –  Apr 23 '14 at 09:40
  • @Rahul: How does it not change the final value? How would the limits of integration NOT change: they are still $0 \le \theta \le 2\pi$ and $0 \le r \le 1$? Would you please expound on how "it all works out"? –  Apr 23 '14 at 10:06
  • The orientation does not matter. Whether $x = r\cos(\theta)$ or $x = r\sin(\theta)$ the final value of the integral is the same. You simply chose a different parametrization than Stewart. See my answer which shows that it works no matter which you choose for $x$ and $z$ as long as $x^2 + z^2 = r^2$. – Brad May 04 '14 at 02:46
  • @Brad 'the final value of the integral is the same': Isn't this true only for this particular problem? I'm asking in general. –  May 04 '14 at 12:20

3 Answers3

1

I will show you how the double integral works out no matter what you select for $z$.

Consider $$\begin{align}I &= \int_0^{2\pi}\!\int_0^1 \!\! r^3 + 2r^3f^2(\theta)\, \mathrm{dr} \, \mathrm{d}\theta \\ &= \int_0^{2\pi}\!\dfrac{1}{4} + \dfrac{1}{2}f^2(\theta)\;\mathrm{d}\theta\end{align}$$

$f(\theta)$ is either $\cos(\theta)$ or $\sin(\theta)$ so $f^2(\theta) = \dfrac{1\pm\cos(2\theta)}{2}$.

$$\begin{align} I &= \int_0^{2\pi}\!\dfrac{1}{4} + \dfrac{1}{2}f^2(\theta)\;\mathrm{d}\theta \\&= \dfrac{\pi}{2} + \dfrac{1}{2}\int_0^{2\pi}\!\dfrac{1\pm\cos(2\theta)}{2}\mathrm{d}\theta \\ &= \dfrac{\pi}{2} + \dfrac{1}{4}\int_0^{2\pi}\!1\pm\cos(2\theta)\;\mathrm{d}\theta \\&= \dfrac{\pi}{2} + \dfrac{1}{4}\int_0^{2\pi}\!1\;\mathrm{d}\theta\pm\int_0^{2\pi}\!\cos(2\theta)\;\mathrm{d}\theta \\ &=\pi\pm \int_0^{2\pi}\!\cos(2\theta) \; \mathrm{d}\theta \\&= \pi\end{align}$$

So you can see that it does work out whether or not you set $z = \sin(\theta)$ or $z = \cos(\theta)$.

Brad
  • 5,156
  • 2
  • 19
  • 50
0

In this question you have to integrate over the whole disk. The best way there is to use the polar coordinates. The normal to the disk is on the direction $-j$ so we have to reverse the orientation as follows

enter image description here

so we take $x=r\sin \theta, z=r\cos \theta, x^2+z^2=r^2$ and integrate from $r=0$ to $r=1$. So the integrand is $$-(x^2+z^2)-2z^2=-[x^2+z^2+2z^2]=-[r^2+2z^2]=-[r^2+2r^2\cos^2\theta]$$ If we take $r=1$ we only consider the boundary of the disk while we have to consider the interior also.

Semsem
  • 7,651
  • +1. Thank you very much! You've found my problem: The normal to the disk is on the direction −j so we have to reverse the orientation as follows. Would you please explain some more? I didn't realise this so am interested in more detail. –  Apr 11 '14 at 15:25
  • Would you please respond in your answer (and not as a comment)? –  Apr 11 '14 at 15:29
0

If we parametrize with $x=r\cos\theta$ and $z=r\sin\theta$, then when $\theta$ increases from $0$ to $2\pi$, the graph created is a circle, but it is oriented clockwise whereas a standard (coherent) orientation would be anticlockwise, this is why we get the normal $-j$ rather than $j$.

But if we re parametrize with $x=r\sin\theta$ and $z=r\cos\theta$. When $\theta$ increases from $0$ to $2\pi$ the graph created is a circle, but this time it is oriented anticlockwise, and thus has the normal $j$.

A coherent orientation is one where, when we move around the boundary, if we were "standing" on the boundary, the enclosure must always be on our left hand side, so for a circle the coherent orientation is anticlockwise.

Imagine the orientation was clockwise, then when we "stand" on the bounday, and move around the circle clockwise, the interior of the circle is no longer on our left.

With regards to "anticlockwise", I was looking from the green direction, because this corresponds to the normal $n=-j$.

Ellya
  • 11,783