9

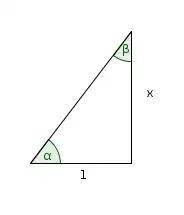
Verify the identity: $\tan^{-1} x + \tan^{-1} (1/x) = \frac\pi 2, x > 0$

$$\alpha= \tan^{-1} x$$

$$\beta = \tan^{-1} (1/x)$$

$$\tan \alpha = x$$

$$\tan \beta = 1/x$$

$$\tan^{-1}[\tan(\alpha + \beta)]$$

$$\tan^{-1}\left [{\tan\alpha + \tan\beta\over 1 - \tan\alpha \tan\beta} \right]$$

$$\tan^{-1}\left[ {x + 1/x\over 1- x/x }\right]$$

$$\tan^{-1}\left[{x + (1/x)\over 0} \right]$$

I can't find out what I'm doing wrong..

Martin Sleziak
  • 53,687
KKendall
  • 869

7 Answers7

15

Hint: When you want to prove that something smooth is constant, use derivatives.

details: if $f(x) = \arctan x + \arctan\frac 1x$ then $$ f'(x) = \frac 1{1+x^2} + \frac 1{1+\left(\frac 1x\right)^2}\times \left(-\frac{1}{x^2}\right) =0 $$ then $f(x) = f(1) = 2\arctan 1 = \frac\pi 2$ on the interval $\{x>0\}$.

The problem of your method is that the formula you are using is true only when $$ \alpha , \beta, \alpha + \beta \neq \frac\pi 2 \mod \pi $$

mookid
  • 28,236
9

An easy, mostly graphical proof: $\tan\alpha=x$, $\tan\beta=\frac1x$, and $\alpha+\beta=\frac\pi2$.

Triangle

The reason you get a division by zero in the argument of arctan is that $\displaystyle\lim_{\varphi\to\frac\pi2}\tan\varphi=\pm\infty\approx\tfrac10$. So, in very informal notation, you could say that $\tan^{-1}(\infty)=\tfrac\pi2$, and that your calculation in a way make sense.

Jonas Granholm
  • 466
  • Can you also do this if $x<0$? I mean, lengths of sides of triangles are always positive... is there a way to do this argument anyway? – learner Aug 21 '15 at 10:28
  • It's only informal if you are unfamiliar with the relevant formalism. $\arctan(\pm \infty) = \pm \pi/2$ is quite standard in real (not complex) settings as soon as one is familiar with the extended real numbers. –  Aug 22 '15 at 00:05
6

You're basically trying to compute $\tan(\pi/2)$, which doesn't exist.

If you set $\beta=\arctan(1/x)$, then $\tan\beta=1/x$, that is $$ x=\cot\beta=\tan\left(\frac{\pi}{2}-\beta\right) $$ Therefore $$ \arctan x=\arctan\tan\left(\frac{\pi}{2}-\beta\right)=\frac{\pi}{2}-\beta $$ by the hypothesis that $x>0$, so that $0<\arctan(1/x)<\pi/2$.

egreg
  • 238,574
5

Assume $x>0$, then

\begin{align}&\tan^{-1} x +\tan^{-1} \dfrac1x \\\\=&\tan^{-1} x +\tan^{-1}\dfrac1{\tan\tan^{-1} x} \\\\=&\tan^{-1} x +\tan^{-1}\cot \tan^{-1} x \\\\=&\tan^{-1} x +\tan^{-1}\tan(\dfrac{\pi}2- \tan^{-1}x) \\\\=&\tan^{-1} x +\dfrac{\pi}2- \tan^{-1}x\qquad\qquad\qquad \left(\because\text{for $x>0$,}\;\dfrac{\pi}2- \tan^{-1}x\in\left(0,\dfrac{\pi}2\right)\right) \\\\=&\dfrac{\pi}2. \end{align}

Alraxite
  • 5,647
4

One may also use complex numbers: We are multiplying two complex numbers with argument $\frac{1}{x}$ and $x$.

So, we desire to show that $\arg((1 + ix)(x + i)) = \frac{\pi}{2}$

We expand the product to get $(x^2 + 1)i$ -- since there is no real part and the imaginary part is $> 0$, the argument is $\frac{\pi}{2}$

MT_
  • 19,603
  • 9
  • 40
  • 81
4

Yet another possibility:

You want $y+z$ for $y,z$ satisfying $\sin y / \cos y=\cos z/\sin z$. Since $\sin y=\cos(\pi/2-y)$ it follows that $z=\pi/2-y$.

JPi
  • 4,562
0

In addition to that which was exposed, I want to say the following:

$\cot(\tan^{-1}x ) = \tan(\pi/2 - \tan^{-1}x)$

Let's prove it:

First, observe that $\cot(\tan^{-1}x) = \cot(\tan^{-1}x + \cot^{-1}x -\cot^{-1}x ) = \cot(\pi/2 -\cot^{-1}x) $ (I)

since $\tan^{-1}x+\cot^{-1}x = \pi/2 $ (II)

But, observe that from equation (I) and also that $\cot(\pi/2 - x) = \tan x$, that $\cot(\pi/2 -\cot^{-1}x) = \tan(\cot^{-1}x).$

Now, we conclude (II).

João Víctor Melo
  • 424